WolframAlpha în limba rusă cum să se extindă funcția într-o serie Fourier
Cum să se extindă funcția într-o serie Fourier
Extinderea funcțiilor în serie Fourier este folosit destul de des, pentru că în această formă este convenabil să se diferențieze, integra, utilizează argumentul de offset al funcției, și funcțiile de convoluție. În ciuda faptului că procedura pentru extinderea seriei Fourier, chiar și în cel mai simplu caz poate fi destul de consumatoare de timp, sistemul de Wolfram Alpha, de regulă, face față cu ușurință această sarcină.
Reprezentat în seria Fourier a formei trigonometrice și exponențială (complex):
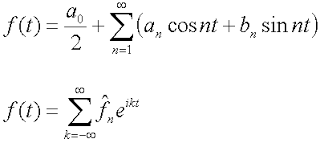
In primul exemplu de realizare, deoarece sistemul bază de descompunere este sinus și cosinus utilizate. Dar, atunci când se lucrează cu serii Fourier în schimb este mai convenabil să se utilizeze exponent al unui argument imaginar. Așa se pare, Wolfram Alpha a preferat a doua opțiune.
Cel mai simplu mod de a extinde funcția într-o serie Fourier - trimite o cerere ca serie Wolfram Alpha Fourier [argumentul funcției, numărul de termeni ai seriei]. De exemplu,
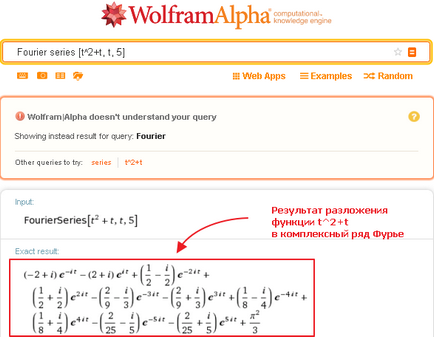
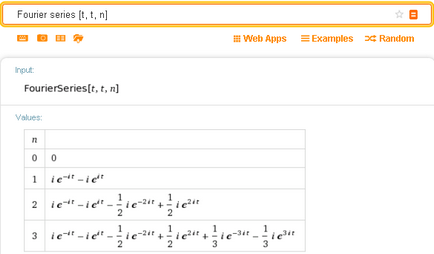
Rezultatele obținute, după cum este necesar, a prezentat condițiile expansiunii cincea cameră inclusiv; coeficienții de exponent sunt grade conjuge numere complexe conjugate.
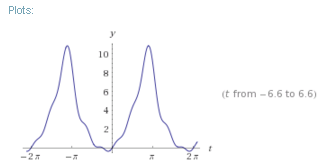
În același timp Wolfram Alpha oferă o reprezentare grafică a apropierea unei serii Fourier funcții date (aici, partea centrală a graficului aproximează parabolică predeterminat):
Chiar mai particular aproximare clar Fourier poate fi văzut în rezultatele acestei interogări (care aproximează o serie Fourier drept):
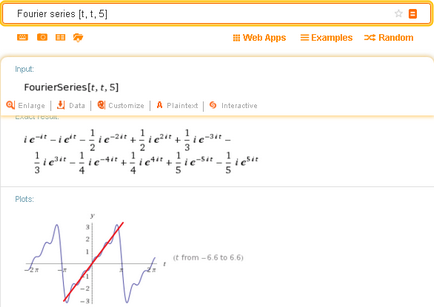
Introducerea unei anumite funcții într-o serie Fourier de formă trigonometrice este afișată în cea mai mică parte a eliberării (aici - pentru al doilea exemplu):
Apropo, în ciuda faptului că problema de mai sus a fost sistemul: „Wolfram | Alpha nu înțelege interogare Se afișează în loc ca rezultat pentru interogarea :. Fourier“, - ceea ce înseamnă „Sistemul nu înțelege solicitarea dvs. prezintă rezultatele corespunzătoare pentru interogarea: Fourier. „nu te lasa pacalit de aceasta;) la cerere“ Fourier“, care își propune să utilizeze sistemul, va fi retrasă sau informații biografice despre matematicianul Jean-Baptiste-Joseph Fourier (matematician). o transformată Fourier a funcției Fourier [t ^ 2 + t]; în funcție de faptul dacă ai pus între cuvântul „Fourier“ și colțarul diferența sau nu.
În cazul în care cererea nu specifică o serie de expansiune Fourier este în mod clar numărul de membri ai n, atunci sistemul Wolfram Alpha implicit afișează patru opțiuni pentru n de la 0 la 3, și numai pentru forma complexă a seriei Fourier:
Opțiuni suplimentare de extindere pentru n mai mare de 3 poate fi obținută instantaneu folosind butonul „More“. Dar acest lucru este valabil numai pentru reprezentarea grafică a rezultatelor:
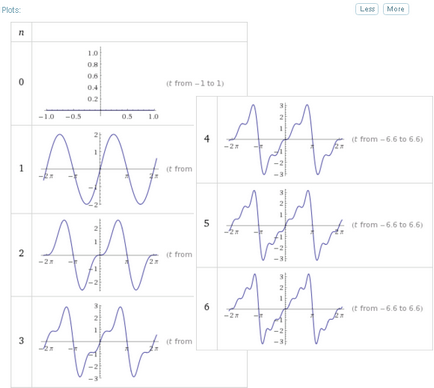
Astfel, pentru a obține descompunerea funcțiilor în serie Fourier trigonometrice, este necesar să se solicite serii Fourier în mod explicit specifica numărul de termeni în expansiune.
Ce se poate face, în cazul în care sarcina nu este de a găsi seria Fourier, coeficienții seriei Fourier?
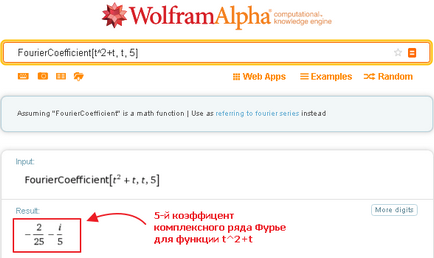
În primul rând, puteți utiliza cerere FourierCoefficient [argument expresie, n]. în care sistemul Wolfram Alpha emite coeficientul n-lea al expansiunii expresiei în seria Fourier complexă.
De exemplu, coeficientul de expansiune expresie a 5 (t ^ 2 + t) într-o serie Fourier poate fi preparată după cum urmează:
În cazul în care, cu toate acestea, nu specifică în mod explicit n, atunci interogarea va afișa o expresie generală pentru coeficientul n-lea a seriei Fourier a expresiilor:
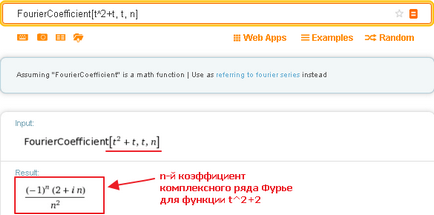
În plus, Wolfram Alpha apoi afișează, de asemenea, un tabel de coeficienți din seria Fourier complexe (până la termen de 15 mii, inclusiv, dacă faceți clic pe „Mai mult“):
În această scurtă trecere în revistă, nu am menționat cum să se extindă funcția într-o serie Fourier de sinus și cosinus, sau cum să utilizeze calculatorul pentru Sisteme Fourier Wolfram Alpha, și a spus nimic despre seria Fourier bidimensională. Toate acestea - tema posturile mele viitoare. Stai cu ochii pe blog.