Piramidele, în care toate muchiile laterale sunt

Luați în considerare proprietățile piramide, în care toate marginile laterale sunt egale, cu desenele corespunzătoare.

Dacă toate marginile laterale ale piramidei sunt egale, vârful piramidei este proiectată în centrul cercului de bază despre descris.

Triunghiurile dreptunghiulare formate prin înălțimea piramidei, marginile laterale și proiecțiile lor (egală cu raza cercului circumscris) sunt egale. Prin urmare, de asemenea,

- toate marginile laterale ale piramidei pentru a forma un plan de bază unghiuri egale;

- toate colțurile care formează marginile laterale ale piramidelor, cu o înălțime egală.

Rezolvarea problemelor într-o piramidă, în care toate marginile laterale sunt egale (sau toate nervurile laterale formează unghiuri egale cu baza piramidei sau înălțimea piramidei) începe cu desen.

În cazul în care baza piramidei - triunghi.

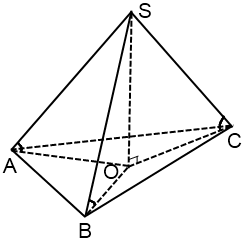
Centrul cercului un triunghi înclinat acut situată în interiorul triunghiului.

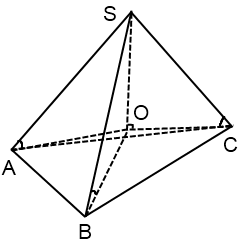
Centrul de cerc descris despre triunghi obtuz se află în afara triunghiului.

Figura unghi obtuz - unghiul B.

Raza cercului circumscris despre un triunghi ascutitunghic sau în unghi obtuz arbitrare ABC pot fi găsite prin investigarea teoremei sine:

sau formula

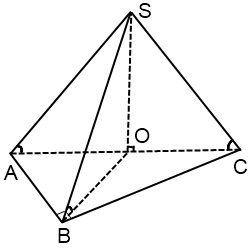
Fi in centrul unui triunghi dreptunghic în jurul cercului este în mijlocul ipotenuzei.

Raza cercului de bază descris despre în acest caz este

unde c - ipotenuzei.

Prin urmare, pentru un anumit triunghi ABC cu unghiul drept B

În cazul în care baza piramidei - un paralelogram

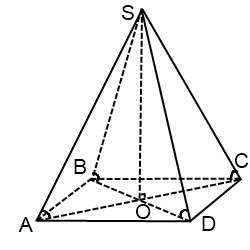
Dintre toate paralelograme descrie un cerc poate doar aproximativ dreptunghi (pătrat - un caz special). Prin urmare, dacă o problemă se spune că piramida toate marginile laterale sunt egale, sau toate nervurile laterale sunt la fel de înclinați spre suprafața de bază, sau toate marginile laterale formează cu înălțimea piramidei unghiuri egale, iar în partea de jos - un paralelogram, atunci acest lucru poate fi doar un dreptunghi (pătrat) .

Acesta este centrul dreptunghiului în jurul cercului - punctul de intersecție al diagonalelor. În consecință, raza R egală cu jumătate din diagonala dreptunghiului.

În cazul în care baza piramidei -trapetsiya

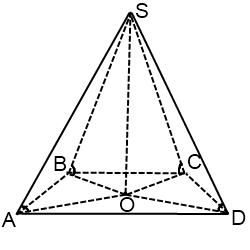
Dintre toate trapezelor poate descrie doar un cerc despre un trapez isoscel.

Raza cercului circumscris atragatori ca raza cercului unul dintre triunghiuri ABC ACD sau pe una dintre formulele indicate mai sus.

Dacă trapezului perpendicular pe latura diagonală

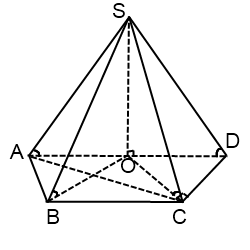
marginile laterale ale piramidei sunt

În acest caz, cercul central descris despre minciunile trapez în mijlocul bazei mai mari, iar înălțimea piramidei situată în fața laterală ce conține această bază mai mare.

Raza R, în acest caz - jumătate ipotenuzei unui triunghi dreptunghic ACD.

În cazul în care baza piramidei - un patrulater arbitrar

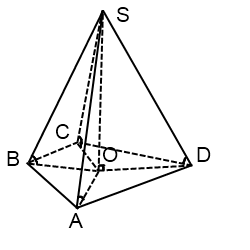
Raza cercului de bază descris cu privire la modul de a găsi raza cercului circumscris cu privire la baza unuia dintre triunghiuri: ABC, BCD, ACD sau DLA.

După cum se descrie în jurul circumferinței patrulaterului nu poate fi decât atunci când suma unghiurilor opuse este de 180 de grade,