Numere complexe selectate probleme

AGENȚIA Federal pentru Educație

STATUL INSTITUȚIE DE ÎNVĂȚĂMÂNT

ÎNVĂȚĂMÂNTUL SUPERIOR

„Universitatea Pedagogică de Stat Voronezh“

SCAUN AGLEBRY și geometria

lucrări de calificare finale

Matematica de specialitate 050,201.65

(Cu specialitate suplimentară 050202.65 informatică)

Îndeplinită: un student al 5-lea an

2. Numere complexe (probleme selectate)

2.1. Numere complexe în formă algebrică .... ....... .......... ....

2.2. Interpretarea geometrică a numerelor complexe ............ .. ...

2.3. forma trigonometrice de numere complexe

2.4. Aplicarea teoriei numerelor complexe pentru a rezolva ecuațiile de gradul 3 si 4-a ............... .. ...............................................................

2.5. numere și parametri complecși .......... ......................... ....

Programul desigur matematica școală în teoria numerelor introduse prin exemple de seturi de numere naturale, numere întregi, raționale, irațional, adică, pe setul de numere reale, imagini care umplu linia reală întreg. Dar, în stocul clasa a 8-a numerelor reale nu este suficient, rezolvarea ecuațiilor de gradul doi cu discriminant negativ. Prin urmare, este necesar pentru a reface stocul de numere reale folosind numere complexe, pentru care rădăcina pătrată a unui număr negativ are sens.

Alegerea temei „numere complexe“ ca tema de munca mea finală de calificare este faptul că noțiunea unui număr complex se extinde cunoștințele elevilor de sisteme numerice pentru rezolvarea unei clase largi de probleme ca algebric și conținutul geometric de a rezolva ecuatii algebrice de orice grad și rezolvarea problemelor cu parametri.

În această teză de lucru revizuită soluție 82 x obiective.

Prima parte a secțiunii principale „numere complexe“ sunt soluții la probleme cu numere complexe în formă algebrică, operațiile definite de adunare, scădere, înmulțire, împărțire, operație de cuplare pentru numere complexe în formă algebrică, întinderea unității imaginare, modulul numărului complex și descrie, în general luând rădăcina pătrată a numărului complex.

În a doua parte a problemei rezolvată într-o interpretare geometrică a numerelor sau vectori complexe ca puncte în planul complex.

A treia parte se ocupă de operațiunile cu numere complexe în formă trigonometrice. Formula folosită: DeMoivre și extragerea rădăcinii numărului complex.

A patra parte este dedicată rezolvării ecuațiilor de a 3-a și a 4-a.

În rezolvarea problemelor din ultima parte a „numerelor complexe și parametrii“ sunt folosiți și asigurate informațiile date în părțile anterioare. seria Heads sarcini este dedicat definirea familiilor de linii în planul complex, definit de ecuațiile (inegalități) cu parametrul. Ca parte a exercițiului ar trebui să rezolve ecuația cu un parametru (peste C). Există locuri de muncă, în cazul în care variabila complexă respectivă îndeplinește simultan mai multe condiții. O trăsătură de rezolvare a problemelor acestei secțiuni este de a reduce cele mai multe dintre ele la soluția de ecuații (inegalități, sisteme) de gradul al doilea, irațional, trigonometrice, cu un parametru.

O prezentare caracteristică a materialului a fiecărei părți este de intrare baze teoretice inițiale și, ulterior, aplicarea practică a acestora în rezolvarea problemelor.

La sfârșitul tezei este o listă de literatură utilizată. Cele mai multe dintre ele sunt destul de detaliate și disponibile prezintă materialul teoretic discutat unele probleme și soluții sunt date sarcini practice pentru auto-determinare. De remarcat că pe surse, cum ar fi:

1. Gordienko NA Belyaeva ES Firstov VE Serebryakov IV Numere complexe și aplicațiile lor: manual. [10]. manual Materialul este prezentat sub formă de prelegeri și exerciții practice.

2. DO Shkliarsky NN Chentsov Yaglom IM Probleme selectate și teoreme matematice elementare. Aritmetică și algebră. [21] Cartea 320 conține sarcini relevante pentru algebra, și teoria numerelor aritmetice. Prin natura lor, aceste provocări diferă semnificativ de sarcinile școlare standard.

2. Numere complexe (probleme selectate)

2.1. Numerele complexe sunt algebric

Solutia de multe probleme în matematică, fizică reduce la soluția de ecuații algebrice, adică, ecuațiile formei

,

în cazul în care A0. a1. ..., o sunt numere reale. Prin urmare, studiul ecuatiilor algebrice este una dintre cele mai importante întrebări din matematică. De exemplu, rădăcinile reale ale ecuației pătratice nu are nici o discriminant negativ. Cea mai simplă astfel de ecuație este ecuația

.

Pentru ca această ecuație are o soluție, este necesar să se extindă setul de numere reale prin atașarea la ea rădăcina ecuației

.

Notam rădăcină prin

. Astfel, prin definiție,

,

.

Se numește unitate imaginară. Cu acesta, și cu o pereche de numere reale

expresie pregătită a formei

.

Expresia rezultată se numește numere complexe, deoarece acestea conțin atât reale și părțile imaginare.

Astfel, numerele complexe sunt numite expresii ale formei

,

- numere reale, și

- un simbol care satisface

Se numește partea reală a unui număr complex

- partea sa imaginară. Pentru simbolurile utilizate denumirile lor

,

.

Numere complexe de forma

Acestea sunt numere reale și, prin urmare, o multitudine de numere complexe cuprinde un set de numere reale.

Numere complexe de forma

numit pur imaginar. Două numere complexe de forma

a spus să fie egal în cazul în care sunt părțile reale și imaginare, adică, dacă egalitati

,

.

intrare algebrică a numerelor complexe vă permite să efectuați operații asupra lor de regulile obișnuite de algebră.

Suma a două numere complexe

este un număr complex

.

.

Scrierea unui nenulă număr complex z ca

Se numește formă trigonometrice de număr complex z. Numărul r este numit modulul unui număr complex z, iar numărul # 966; aceasta se numește argumentul unui număr complex și este notat Argz.

formă trigonometrică a unui număr complex - (formula lui Euler) - formă exponențială a numărului complex:

.

Într-un număr complex z sunt infinit mai multe argumente: dacă # 966; 0 - orice argument z, atunci restul poate fi găsit cu ajutorul formulei

.

Pentru un număr complex

argument și forma trigonometrică nu sunt detectate.

argument Astfel, nenulă unui număr complex

este orice soluție a sistemului:

valoare # 966; argumentul unui număr complex z, satisfăcând inegalitățile

, Acesta a numit principal și argz desemnat.

Argumentele Argz și argz legate de

(5) este o consecință a sistemului (3), astfel încât toate argumentele numărului complex

satisfac ecuația (5), dar nu toate soluțiile # 966; Ecuația (5) reprezintă numărul de argumente z.

Valoarea principală a argumentului unui număr complex nenul

este dată de:

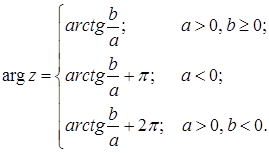
Formula de înmulțire și împărțire a numerelor complexe în formă trigonometrică sunt după cum urmează:

Atunci când ridicarea o putere naturală a numărului complex utilizat formula DeMoivre:

Formula este utilizată la extragerea rădăcinii unui număr complex: