Exemple derivate de soluții

anterior ◈ următoarea

Găsiți intervale de creștere și descreștere, extreme de funcții:

$Exemple derivate de soluții$

Pentru a găsi punctele critice găsi derivata funcției inițiale și setați-o egală cu zero.

$Exemple derivate de soluții$

Derivata dispare la punctele

$Exemple derivate de soluții$

Aplicarea metodei de intervale determinate de semnul derivatului la intervalele respective.

Exemple derivate de soluții

Astfel crește cu funcții

$Exemple derivate de soluții$

și scade pentru

$Exemple derivate de soluții$

Extremele de funcții:

$Exemple derivate de soluții$

punctul maxim,

$Exemple derivate de soluții$

punctul de minim.
Valorile funcției la extremelor:

$Exemple derivate de soluții$

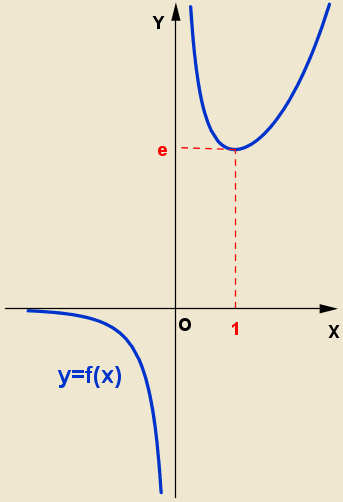
Schița grafic arata ca:

Exemple derivate de soluții

Găsiți intervale de creștere și descreștere, extreme de funcții:

$Exemple derivate de soluții$

Această funcție este definită pentru

$Exemple derivate de soluții$

Calculăm derivatul său pentru identificarea punctelor critice și intervale de semn constant al derivatului.

$Exemple derivate de soluții$

Rețineți că, la punctul

$Exemple derivate de soluții$

și în vecinătatea sa funcția inițială nu există.
La punctul

$Exemple derivate de soluții$

nu există nici o funcție original sau derivatul său. Astfel,

Exemple derivate de soluții

Astfel crește cu funcții

$Exemple derivate de soluții$

și scade pentru

$Exemple derivate de soluții$

Extremum a funcției:

$Exemple derivate de soluții$

punctul maxim. Valoarea funcției în acest moment:

$Exemple derivate de soluții$

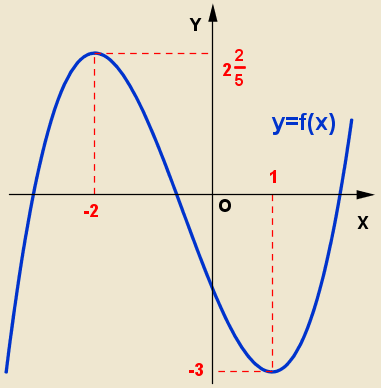
Schița grafic arata ca:

Exemple derivate de soluții

Găsiți intervale de creștere și descreștere, extreme de funcții:

$Exemple derivate de soluții$

Această funcție este definită pentru

$Exemple derivate de soluții$

Calculăm derivatul său pentru identificarea punctelor critice și intervale de semn constant al derivatului.

$Exemple derivate de soluții$

Punctul critic este

$Exemple derivate de soluții$

Iar la punctul

$Exemple derivate de soluții$

funcția inițială și derivatul său nu există,
și litera

$Exemple derivate de soluții$

se anulează instrumentelor derivate. Noi folosim metoda intervalului pentru a găsi semnul derivat
la intervale adecvate.

Exemple derivate de soluții

Astfel crește cu funcții

$Exemple derivate de soluții$

și scade pentru

$Exemple derivate de soluții$

Extremum a funcției:

$Exemple derivate de soluții$

punctul de minim. Valoarea funcției în acest moment:

$Exemple derivate de soluții$

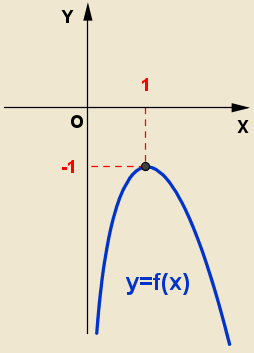
Schița grafic arata ca:

Exemple derivate de soluții

anterior ◈ următoarea