Dublă sarcină - elaborarea normelor - programarea liniară

Prezintă regulile de a face probleme duale. Sunt considerate simetrice, asimetrice și perechi mixte. exemple de Analizate elaborarea problemelor duale.

Dual sau conjugat problemă de programare liniară au proprietatea că soluțiile de la una dintre sarcinile pe care le puteți obține alte sarcini. Aici ne uităm la regulile de elaborare a unor probleme duale.

problemă dublă Symmetric

Luați în considerare problema de programare liniară cu variabile non-negative și inegalitățile de constrângerile sistemului de forma următoare:
(1.1);
(1.2)
Aici. există unele numere. Toate sistemele de linie (1.2) este inegalitatea caracterelor.

Dual Problema este:
(2.1);
(2.2)
Aici, toate linia de sistem (2.2) este inegalitatea de caractere. Coeficienții de matrice ale sistemului de constrângere (2.2) este matricea sistemului transpuse (1.2). Acesta cuprinde rânduri și coloane. Dual problema este variabilă. Toate variabilele sunt non-negativ.

Problema inițială (1) este adesea menționată ca o provocare directă, și problema (2) - dublă. În cazul în care începe să ia problema (2), apoi (2) va conduce sarcina, iar sarcina (1) - dublă. Sarcini (1) și (2) sunt numite sarcini duble simetrice.

Astfel, o problemă dublă simetrică poate fi format numai în cazul în care toate variabilele problemei inițiale și sistemul de constrângere non-negativ nu conține ecuații. Dacă vă căutați pentru un maxim al funcției obiectiv, inegalitatea trebuie să fie transformat în forma. Dacă sunteți în căutarea cel puțin, inegalitățile trebuie să fie transformat în forma. Pentru a schimba semnul, trebuie să multiplice ambele părți ale inegalității de -1.

Exemplu de problemă dublă simetrică

Având în vedere problema de programare liniară:
;

Creați dublă problemă.

Problema inițială este sarcina de a găsi un minim. Prin urmare, toate semnele de inegalitate ar trebui să aibă. Prima și a treia inegalitățile conțin semnul. multiplicați-le -1:

Rescriem sistemul de restricții, indicând în mod clar coeficienții variabilelor:

constrângeri de sistem matrice coeficient are forma:

Transpune această matrice. Asta este, prima linie poate fi scrisă ca prima coloană, pe al doilea rând poate fi scris ca a doua coloană, al treilea rând poate fi scris ca a treia coloană.

Dual Problema este:
;

problemă dublă asimetrica

Provocarea pentru maxim

Luați în considerare problema canonică de programare liniară cu variabile non-negative și constrângerile maxime ale rapoarte egale sistemului:
(3.1);
(3.2)
Aici. există unele numere. Toate liniile de sisteme (3.2) sunt egalitati. Toate variabilele sunt non-negativ.

Dual Problema este:
(4.1);
(4.2)
Aici, toate linia de sistem (4.2) este inegalitatea de caractere. Coeficienții de matrice ale sistemului de constrângere (4.2) este matricea sistemului transpuse (3.2). Dual problema este variabilă. Variabilele pot fi pozitive sau negative.

Spre deosebire de problemele pereche asimetrice (3) și (4) ale unei perechi simetrice (1) și (2) că constrângerile de sistem (3.2) conține doar egalitate și în sistem (4.2) nu există condiții nonnegativeness variabile.

Sarcina cel puțin

Acum, ia în considerare problema canonică de programare liniară la minimum:
(5.1);
(5.2)

Dual Problema este:
(6.1);
(6.2)

sistem de restricție (6.2) este diferit de (4.2), care sunt semne de inegalitate.

Comunicarea cu o pereche simetrică de probleme duale

Ne arata ca problemele de cuplu dezechilibrat (3) - (4) pot fi preparați din perechi simetrice (1) - (2).

Deci, să presupunem că avem o problemă directă cu funcția obiectiv
(3.1)
și limitările sistemului
(3.2)
Fiecare ecuație poate fi reprezentată de două inegalități:

Inegalitățile cu semne multiplica de -1:

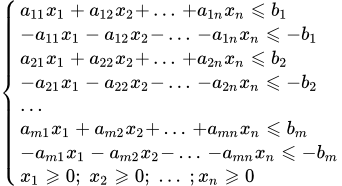
Sistemul are limitări inegalități.

Prin (1) - (2) obținem problema dublă:
;

dublă problemă are o variabile non-negativ:
.
Este ușor de observat că aceste variabile sunt o parte a problemei sub forma diferențelor
.

Facem schimbarea
.
Deoarece ambele. variabilele pot fi atât pozitive, cât și negative.

Și obținem problema duală (4):
(4.1);
(4.2)

Dacă luăm pentru problema originală (4), care îndeplinește toate etapele în ordine inversă, obținem problema duală (3).

În același mod poate fi problema (5) pentru a primi problema duală (6) și problema (6) pentru a primi problema duală (5).

problemă mixtă

Acum, ia în considerare problema mixtă.

Să presupunem că avem o problemă directă (1) la maxim, într-un sistem care limitează rândul i-lea este o egalitate. Apoi dubla problema are forma (2), cu o singură excepție - variabila poate fi pozitiv sau negativ. Adică, nu există nici o restricție.

Același lucru se întâmplă dacă avem o problemă directă (2), cel puțin în sistem, care limitează rândul i-lea este o egalitate. Problema dublă are forma (1), cu o singură excepție - variabila poate fi de nici un semn.

Acum, să presupunem că avem o problemă directă (1) la maxim, dar nu există nici o restricție. Aceasta este, variabila poate fi pozitiv sau negativ. Apoi, problema dublă are o formă (2), cu o singură excepție - lea sistem de restricție rând este egalitate.

În cele din urmă, să presupunem că avem o problemă directă (2) la minimum, dar nu există nici o restricție. Apoi, problema dublă are forma (1), cu o singură excepție - lea sistem de restricție rând este egalitate.

Toate acestea ne permite să formulăm regulile de a face probleme duale.

Regulile de luare a problemelor duale

1. Pentru problema inițială la maxim, toate restricțiile de inegalitate ale sistemului produce:
.
Pentru problema inițială la un nivel minim, toate inegalitatea se reduce la:
.
Dacă doriți să schimbați semnul, apoi multiplica ambele părți ale inegalității de -1.
2. Asigurați-vă o problemă dublă în același mod ca și pentru sarcinile pereche simetrice.
3. Dacă problema inițială, constrângerile-lea ale liniei de sistem este egalitate, atunci vom trece din starea de non-negativitate lea variabilă a problemei duale.
4. În cazul în care problema originală, nu există nici o condiție de bază non-negativitate pentru variabila i-lea. în rândul lea al problemei dublă schimbare semnul inegalității pe semnul egal.

Exemplu de problema duală mixt

Având în vedere problema de programare liniară:
;

Creați dublă problemă.

Funcția obiectiv are un membru liber 5. Pentru a aduce la forma (2.1), introducem o variabilă și se adaugă egalitatea. Apoi, problema devine:

Această problemă este o problemă de a găsi un minim. Prin urmare, toate semnele de inegalitate ar trebui să aibă. inegalitățile terțe conțin semn. Prin urmare, vom multiplica de -1:

Rescriem sistemul de restricții, indicând în mod clar coeficienții variabilelor:

constrângeri de sistem matrice coeficient are forma:

Transpune această matrice. Asta este, prima linie poate fi scrisă ca prima coloană, pe al doilea rând poate fi scris ca a doua coloană, și așa mai departe.

Am construit problema dublă pentru ambele perechi simetrice.
;

Ca și în problema originală 1, 2 și rândul a 4 sunt limitările ecuațiile sistemului, variabilele din problema duală. și poate avea orice semn. variabilă non-negativ este pur și simplu. Prin urmare, condițiile de non-negativitate variabilelor sunt de forma:
.

Ca și în problema inițială, și variabilele pot avea semne arbitrare, 3 si 4 constrângerile sistemului de linii ale problemei duale sunt egalități.

Astfel, problema dublă are forma:
;

Din a patra ecuație. Înlocuiți variabila și valoarea sa, vom multiplica de-al treilea rând de -1.