Cum de a construi simetrie

Pentru a răspunde la această întrebare, trebuie mai întâi să definim - ce parametri secțiunea specificată.
Să fie linia de intersecție l plan de bază con cu planul de secțiune și punctul O, care este înălțimea punctului de intersecție al conului cu secțiunea sa transversală.

Figura 1 ilustrează construcția. Primul pas al secțiunii de construcție - se realizează prin secțiunea centrală a diametrului său, extins la l perpendicular pe această linie. Rezultatul este un punct de L. Apoi, prin punctul O trage un LW drept, și de a construi două ghid de con, situată pe secțiunea principală și O2M O2c. Intersecția acestor ghiduri sunt punctul Q și punctul deja prezentat W. Acestea sunt primii doi termeni ai secțiunii transversale dorite.

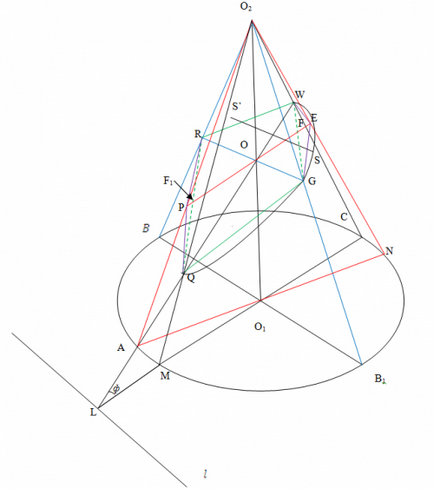
Acum dețin diametrul conului de bază perpendicular MS BB1 și desenați formatoare secțiunii perpendiculare și O2V O2V1. În această secțiune prin punctul O trage un RG drept, paralel cu BB1. T.r. și t.G - încă două puncte ale secțiunii dorite. În cazul în care conturul secțiunii sferic este cunoscut, ar fi putut fi construite în acest stadiu. Cu toate acestea, acest lucru nu este o elipsă, dar ceva eliptică, având o simetrie despre segment QW. Prin urmare, este necesar să se construiască secțiune cât mai multe puncte, conectându-le în continuare buna curba pentru a obține schița cea mai fiabilă.

Construi o secțiune punct arbitrar. Pentru a realiza acest lucru în diametru con de bază arbitrară AN și de a construi ghiduri adecvate și O2A O2N. Bețivan prin linia O punct prin PQ și WG, până la intersecția cu piesele nou construite în punctele P și E. Acestea sunt două mai multe dintre punctele de intersecție dorite. Continuând în același mod și, puteți apela orice număr de puncte dorite.

Cu toate acestea, procedura de obținere a acestora poate fi un pic mai ușor folosind simetrie în raport cu QW. Acest lucru poate fi în secțiunea din titlu a planului de a deține SS direct“, RG paralele până la intersecția lor cu suprafața conului. Construcția este completată prin rotunjirea poligon construit de acorduri. Suficient pentru a construi jumătate din secțiunea transversală dorită datorită simetriei deja menționat în ceea ce privește QW.

Găsiți rădăcinile unei ecuații pătratice. Ecuația pătratic cu o singură necunoscută, după cum urmează: AX2 + bx + c = 0. Aici x este necunoscut dorit; Coeficienții a, b și c sunt cunoscute, în care nu trebuie să fie 0. Dacă vom împărți ambele părți ale ecuației pătratice predeterminate pentru un factor, de a primi ecuația pătratică redus de forma x2 + px + q = 0, unde p = b / a și q = c / a. Cu condiția ca unul dintre coeficienții b sau c, sau ambele sunt egale cu zero, o ecuație pătratică obținută ai numit incomplet.

Găsiți discriminante, care se calculează conform formulei: b2-4ac. În acest caz, dacă valoarea D este mai mare decât 0, ecuația pătratică are două rădăcini reale; în cazul în care D = 0, rădăcinile reale se găsesc egale între ele; dacă D

O reprezentare grafică a unei funcții pătratice este o parabolă. Identificarea de date suplimentare pentru a reprezenta grafic această funcție pătratică: direcția „ramuri“ ale parabolei, vârful său, și ecuația axei de simetrie. Dacă a> 0, atunci „ramura“ a parabolei vor fi îndreptate în sus (în caz contrar, „ramura“ va fi orientată în jos).

Pentru a determina coordonatele vertexul parabolei obține x conform formulei: -b / 2a, apoi înlocui valoarea „X“ din ecuația pătratică pentru a obține valori ale lui y.

În fine, axa de simetrie ecuație depinde de valoarea coeficientului c în ecuația de gradul doi original. De exemplu, dacă un anumit pătratic ecuația y = h2-6h + 3, axa de simetrie va trece prin, în care x = 3.

Cunoscând direcția „ramuri“ ale parabolei, coordonatele nodurilor sale, precum și axa de simetrie, construi folosind un grafic model predeterminat al ecuației pătratice. Se indică pe grafic reprezentate rădăcini: ele vor fi zero.

Pentru a construi un parabole-model este considerat un caz canonic y = x2.

• Graficele și proprietățile de bază ale funcțiilor elementare
• cum să atragă un grafic cu funcția rădăcină

Proprietățile de simetrie sunt folosite în mod constant în AutoCAD. În acest scop, opțiunea Mirror. Pentru a construi un triunghi isoscel sau trapez isoscel bază inferioară suficient pentru a trage, iar unghiul dintre acesta și lateral. Reflectă-le folosind comanda specificată și extinde părțile la valoarea dorită. În cazul triunghiului va fi un punct de intersecție, și pentru trapez - valorii de referință.

• cum să atragă o simetrie centrală