vectori coplanari

Doi vectori sunt paralele cu același plan se numesc coplanari.

Să presupunem că avem trei vectori $ \ overrightarrow, \ \ overrightarrow $ și $ \ overrightarrow $. atunci

O pereche de vectori $ \ overrightarrow, \ și \ \ $ overrightarrow, $ \ overrightarrow $ și $ \ overrightarrow $ și $ \ overrightarrow $ și $ \ $ overrightarrow coplanare unul cu celălalt.

Dacă doi dintre acești vectori, cum ar fi $ \ overrightarrow, \ și \ \ $ overrightarrow, coliniari, atunci vectorii $ \ overrightarrow, \ \ overrightarrow $ și $ \ $ overrightarrow coplanare.

Dacă $ \ overrightarrow, \ \ overrightarrow $ și $ \ $ overrightarrow se află în același plan, acestea sunt coplanare.

Pentru examinare suplimentară ne amintim următoarea teoremă.

vector de Arbitrare $ \ overrightarrow

$ Poate fi extins în doi vectori non-coliniare $ \ overrightarrow, \ $, si $ \ $ overrightarrow cu doar coeficienții de expansiune, adică,

Teoreme, referitoare la conceptul de coplanaritate a trei vectori

Să se dea o cutie. Găsiți un triplu vectori coplanari descris în paralelipipedului în figura de mai jos.

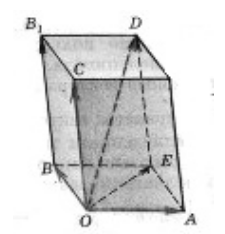
Deoarece vectorii $ \ overrightarrow, \ \ overrightarrow $ și $ \ $ overrightarrow minciună în $ planul (BOA) $, atunci acești vectori sunt coplanare.

Deoarece vectorii $ \ overrightarrow, \ \ overrightarrow $ și $ \ overrightarrow_1> $ minciună în $ planul (BOC) $ atunci acești vectori sunt coplanari.

Deoarece vectorii $ \ overrightarrow, \ \ overrightarrow $ și $ \ $ overrightarrow minciună în $ planul (COE) $, atunci acești vectori sunt coplanare.

Dovedeste ca vectorii coordonatele \ $ din stânga (1 \ 13 \ 2 \ dreapta), \ \ stânga (3 \ -5 \ 2 \ dreapta) și \ (5, 1,4) $ coplanare.

Aplicăm semnul coplanaritate a trei vectori.

De aceea, este vectori coplanari.