Stare perpendicular vector

În acest articol, vom acorda o atenție deosebită condiției a doi vectori perpendiculare în plan și în spațiul tridimensional, precum și găsirea coordonatele vectorului perpendicular pe o pereche sau un set de vectori. Acest subiect este important, deoarece există un număr semnificativ de probleme (de exemplu, provocările asociate cu ecuațiile de linii și avioane), din care soluția se bazează pe constatarea vectorilor perpendiculare pe vectorii cunoscuți.

În primul rând, ne vom face cu condiția necesară și suficientă pentru doi vectori perpendiculari. Apoi, din starea perpendicularitate obținem metoda de constatare vector dat vector perpendicular pe un plan în spațiu. În concluzie, să ne ia în considerare o modalitate de a găsi un vector perpendicular pe ambele doi vectori. Asigurați-vă că pentru a da unele soluții detaliate de exemple.

Navigare în pagină.

O condiție necesară și suficientă pentru doi vectori perpendiculari.

Să ne amintim definiția vectori ortogonali în plan și în spațiul tridimensional.

Doi vectori nenuli sunt numite perpendiculare. dacă unghiul dintre ele este egală cu nouăzeci de grade (radiani).

Ce gânduri sugerează această definiție, atunci trebuie să știți două imagini vectoriale perpendiculare sau nu?

Dacă un anumit punct de pe planul de a întârzia vectori egali vectori date, folosind apoi poate măsura raportorul unghiului între acestea. Acest lucru permite un anumit grad de precizie vectorilor perpendicularitate (dacă a primit nouăzeci de grade unghi atunci când este măsurat). În acest caz, desigur, ar trebui să ia în considerare precizia construcției și precizia de măsurare. O astfel de metodă pentru a determina rectangularitatea a doi vectori ar trebui să fie folosite numai atunci când nu știm nimic despre acești vectori, și au doar imaginea lor în avion.

În practică, de multe ori se dovedesc a avea doi vectori nenuli perpendicularitate, atunci când sunt cunoscute pentru coordonatele lor în sistemul de coordonate rectangulare în plan sau în spațiu. În acest caz, o condiție necesară și suficientă pentru doi vectori perpendiculari. Am afirma ca teorema.

Pentru rectangularitatea doi vectori nenuli și este necesar și suficient ca produsul lor scalar este egal cu zero, și anume, că egalitatea.

Să presupunem că vectorii și sunt perpendiculare. Să demonstrăm egalitatea.

Prin definiția produsului scalar al vectorilor este egală cu produsul dintre lungimile lor de cosinusul unghiului dintre ele. Deoarece vectorii sunt perpendiculare, unghiul dintre ele este egal cu nouăzeci de grade, prin urmare, după cum este necesar.

Ne întoarcem la a doua parte a demonstrației.

Acum ne gândim. Vom demonstra că vectorii și sunt perpendiculare.

Deoarece vectorii și nenulă, rezultă din faptul că. Astfel, cosinusul unghiului dintre vectori este egal cu zero și, în consecință, unghiul este egal, indicând faptul că vectorii și perpendicularitatea.

Astfel, o condiție necesară și suficientă pentru doi vectori perpendiculari este demonstrată.

După cum arată condiția rectangularitate a doi vectori în formă componente?

În produsul scalar în coordonatele am arătat că doi vectori cu coordonatele date și egalitatea plane, cât și pentru cei doi vectori în spațiu. Astfel, o condiție necesară și suficientă a perpendicularității a doi vectori în coordonate este pe un plan și un spațiu tridimensional.

Luați în considerare aplicarea acestor condiții în practică, această soluție a analiza câteva exemple.

dacă vectorii sunt perpendiculare.

Prin starea de vectori perpendiculari avem. Să presupunem, atunci, vine de la. Astfel, vectorul - unul dintre vectorii care sunt perpendiculare pe vectorul.

.

In mod similar cautat vector perpendicular pe vectorul dat în spațiul tridimensional.

Pentru vectorul există un set infinit de vectori ortogonali. Vom arăta acest lucru. Lăsați vectorul se află pe linia A. Vom nota cu un plan arbitrar perpendicular pe o linie dreaptă o. Apoi, orice vector nenul aparținând unui plan perpendicular pe vectorul.

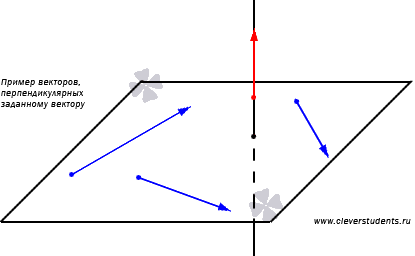
Ne arată modul de utilizare condițiile vectorilor perpendicularitate sunt coordonatele unui vector perpendicular pe un vector dat non-zero.

Lăsați vectorul are coordonatele și. Găsiți-le.

Prin starea celor doi vectori sunt perpendiculare ale egalității. Deoarece vectorul este nenul, atunci cel puțin una dintre coordonatele sale este diferit de zero. Fie (sau puteți lua). Apoi, acesta poate fi împărțit în coordonatele ambelor părți, în același timp, se obține. Astfel, dând coordonatele și valori arbitrare, cel puțin una dintre acestea fiind nenul și calcularea cu formula, obținem un vector perpendicular pe vectorul dat.

Să considerăm următorul exemplu.

Găsiți coordonatele unui vector perpendicular pe vectorul.