sisteme de ecuatii liniare Rezolvarea prin Gauss-Jordan

În general, ecuația liniară este:

Ecuația are o soluție: dacă cel puțin unul dintre coeficienții necunoscutelor este non-zero. În acest caz, orice vector dimensional numit o soluție a ecuației dacă ecuația devine o identitate prin substituirea coordonatele sale.

Caracteristici generale ale rezoluției sistemului de ecuații

Pentru a caracteriza sistemul de ecuații.

1. este o parte dintr-un sistem de ecuații liniare ecuații contradictorii? (Dacă coeficienții, în acest caz, ecuația are forma și se numește inconsistente.)

• În cazul în care sistemul conține contradictorii, un astfel de sistem este incompatibil și nu are soluții

2. Găsiți toate variabilele permise. (Nazyvaetsyarazreshennoy necunoscut pentru sistemul dacă este inclus într-un sistem de ecuații cu un coeficient de +1, iar în celelalte ecuațiile nu este inclus (adică, intra intr-un factor egal cu zero).

• În exemplul nostru, partea necunoscută a primei ecuații cu unitate de coeficient, a doua ecuație nu este inclusă, adică este mai întâi permisă.
• În mod similar - se găsește numai în a doua ecuație și numai în primul.

3. Este sistemul de ecuații permis? (Sistemul de ecuații numite permise. Dacă fiecare ecuație conține permise necunoscute, între care nu există suprapunere)

• Sistemul nostru este permisă, deoarece fiecare ecuație conține permise necunoscute)

Permise necunoscut, luate câte unul din fiecare ecuație a sistemului, formează un set complet de sistem necunoscut permise. (În acest exemplu)

necunoscutelor permise care apar într-un set complet, de asemenea, numit de bază (), care nu sunt incluse în setul - gratuit ().

În general, rezoluția sistemului de ecuații este de forma:

În această etapă, lucrul cel mai important pentru a înțelege ceea ce este permis necunoscut (o parte din baza și libere).

Soluție totală de bază privată

Soluția generală a sistemului autorizat este o colecție de expresii permise necunoscute prin termenii liberi și necunoscutele gratuite:

O soluție particulară a sistemului este soluția, care rezultă din general în valorile particulare ale variabilelor libere și necunoscute.

O soluție de bază se numește o anumită soluție, care rezultă din totalul zero valori ale variabilelor libere.

• Soluție de bază (vector) se numește degenerată. în cazul în care numărul de origine, altele decât zero, mai mic decât numărul de permise necunoscut.
• Soluție de bază se numește non-degenerate. în cazul în care numărul de origine, altele decât zero, egal cu numărul de sistem necunoscut permise incluse într-un set complet.

Teorema (1)

Sistemul permis de ecuații este întotdeauna consecvent (deoarece are cel puțin o soluție); iar în cazul în care sistemul nu este liber de necunoscute (de exemplu, sistemul de ecuații include toate permise în baza) este definit (are o soluție unică); în cazul în care există cel puțin o variabilă liberă, atunci sistemul nu este definit (are infinit mai multe soluții).

Exemplul 1. Găsiți soluția generală, de bază, precum și orice particular al sistemului de ecuații:

1. Verificați dacă rezoluția sistemului?

• Sistemul este permis (ca fiecare din ecuațiile conține permise necunoscute)

2. Includerea în kit-ul permise necunoscut - cate unul din fiecare ecuație.

• În cazul nostru, putem include în setul de permise necunoscut din prima ecuație - și, de la doar a doua ecuație. Aceasta este, un set poate consta din () și ().

3. Notați soluția generală, în funcție de ce permisiuni sunt necunoscute, am inclus în kit-ul.

• să spunem că am inclus un set de necunoscute și apoi soluția generală ar arata astfel:

4. Găsiți o soluție specială. Pentru a face acest lucru, vom echivala variabilele libere pe care nu le-am inclus în setul pentru a echivala cu un număr arbitrar.

• Să presupunem, atunci soluția generală este găsit:

Răspuns: Soluția particular (una)

5. Am găsit soluția de bază. Pentru a face acest lucru, vom echivala variabilele libere pe care nu le-am inclus în set la zero.

Elementare ecuații liniare de transformare

Sistemul de ecuații liniare sunt autorizate să fie echivalente cu sistemele care utilizează transformări elementare.

Teorema (2)

Dacă orice ecuație sistem este înmulțită cu un număr diferit de zero. iar ecuațiile rămase rămân neschimbate, obținem sistemul este echivalentă cu aceasta. (Asta este, dacă vă înmulțiți partea stângă și partea dreaptă a ecuației la același număr veți obține o ecuație echivalentă cu acest lucru)

Teorema (3)

Dacă pentru orice ecuație a sistemului pentru a adăuga mai mult. și tot restul ecuației rămân neschimbate, obținem sistemul este echivalent cu acest lucru. (Asta este, dacă adăugăm cele două ecuații (însumând laturile lor stânga și dreapta), obținem o ecuație de date echivalente)

Corolar teoriei (2 și 3)

Dacă pentru orice ecuație pentru a adăuga un alt multiplicat cu un numar. și tot restul ecuației rămân neschimbate, obținem sistemul este echivalent cu acest lucru.

Formula recalcularea coeficienților

Dacă avem un sistem de ecuații, și vrem să-l transforme într-un sistem de ecuații ne-a permis să ajute în această metodă de Gauss-Jordan.

Transformarea Iordaniei elementului permisiv permite obținerea unui sistem de ecuații pentru necunoscut în ecuația permis camerei. (Exemplul 2).

Transformarea Iordaniei constă în transformări elementare de două tipuri:

1. Ecuația elementului permisiv este împărțit prin aceea că respectivul element (înmulțit cu)
2. Ecuația elementului permisiv este multiplicată cu un factor corespunzător și se adaugă la toate celelalte ecuațiile pentru a elimina necunoscut.

Să presupunem că vrem să facem necunoscutul în ecuația de jos permise necunoscut. Pentru a face acest lucru, trebuie să fie împărțită în, astfel încât suma.

Exemplul 2. recalcula coeficienții

Când împărțirea ecuației cu numărul coeficienților săi sunt recalculate în conformitate cu formulele:

pentru a exclude

din ecuația cu index , Avem nevoie de o ecuație cu un număr înmulțit cu și adăugat în ecuație.

Teorema (4), pentru a reduce numărul de ecuații.

Dacă sistemul de ecuații conține ecuația banal, poate fi eliminat din sistem, se obține astfel un sistem echivalent cu originalul.

Teorema (5) Incompatibilitatea ecuații.

Dacă sistemul de ecuații conține ecuații contradictorii, este inconsistent.

Algoritmul metodei lui Gauss-Jordan

Algoritmul pentru sistemele de ecuații de rezolvare Gauss-Jordan constă într-o serie de etape similare, fiecare dintre care efectuează acțiuni în această ordine:

1. Verificat, nu este sistemul de inconsistente. În cazul în care sistemul conține o ecuație contradictorie, este inconsecvent.
2. Verificat posibilitatea reducerii numărului de ecuații. În cazul în care sistemul conține o ecuație banală, greva lui afară.
3. Dacă sistemul de ecuații este rezolvată, atunci scrie soluția generală a sistemului și, dacă este necesar - soluții private.
4. Dacă sistemul nu este permisă, atunci în ecuația, care nu conține necunoscute permise, permițând elementului selectat și să producă conversie Jordan cu acest element.
5. În plus retransferate la paragraful 1,

Exemplul 3. Pentru a rezolva sistemul de ecuații de Gauss-Jordan.

Find. două generale și două soluții de bază corespunzătoare

Calculele prezentate în tabelul următor:

La dreapta a tabelului arată acțiunile pe ecuațiile. Săgețile indică la care se adaugă elementul permisive ecuația ecuației înmulțită cu un factor corespunzător.

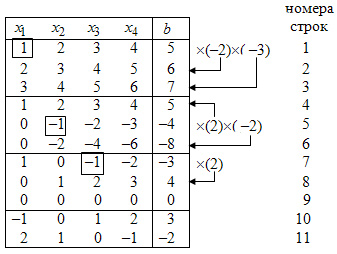
În primele trei rânduri din tabel sunt plasate coeficienții de necunoscut și laturile din dreapta ale sistemului original. Rezultatele primei unității permisive element de conversie Jordan arătate în liniile 4, 5 și 6. Rezultatele celui de al doilea element de conversie Jordan permisiva egal cu (-1) sunt prezentate în rândurile 7, 8, 9. Deoarece a treia ecuație este banală, nu se poate luate în considerare.

Sistemul echivalent admis necunoscut și are forma:

Acum putem scrie soluția generală:

Egalăm variabile libere și zero și obținem.

Pentru a găsi al doilea general și soluția de bază corespunzătoare, care rezultă în rezoluția sistemului în orice ecuație trebuie să selectați orice alt element care permite. (Faptul că ecuația liniară poate include câteva soluții generale și de bază). În cazul în care rezoluția sistemului de ecuații este echivalent cu sistemul original conține necunoscute și ecuații, numărul de decizii comune și relevante ale baza sistemului original este numărul de combinații și. Numărul de combinații poate fi calculat prin formula:

În cazul nostru, suntem Stadii elementul (1), în prima ecuație care permite (linia 7). În continuare este transformarea Iordaniei. Obținem un nou (linii 10-11) a permis c necunoscutelor nou sistem de permise:

Scrieți a doua soluție generală:

Și soluția de bază corespunzătoare.