Rădăcina pătrată a 2 - a

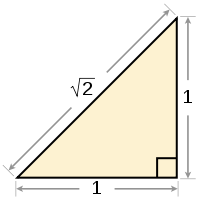
Rădăcina pătrată a 2 este egală cu lungimea ipotenuzei într-un triunghi dreptunghic cu o singură lungime de catete.

Rădăcina pătrată a 2 - un număr real pozitiv. care atunci când este multiplicată cu ea însăși dă numărul 2. Descriere: Dăm valoare de rădăcină de la 2 până la 65 de caractere după virgulă:

213 562 373 1414 095 048 801 688 724 209 698 078 569 671 875 376 948 073 176 679 737 99 ...

rădăcină Geometric 2 poate fi reprezentat ca lungimea diagonalei unui pătrat cu latura de 1 (aceasta rezultă din teorema lui Pitagora). Acest lucru a fost, probabil, prima cunoscut în istoria de număr irațional matematică (de exemplu, un număr care nu poate fi exprimată exact ca o fracție).

Rădăcina pătrată a 2.

O abordare bună și frecvent utilizate într-o fracțiune. În ciuda faptului că numărătorul și numitorul unui întreg din două cifre, acesta diferă de valoarea reală este mai mică decât 1/10000.

tabletă de lut babiloniene cu note.

tabletă de lut Babel (cca 1800-1600 BC ...) dă valoarea aproximativă în sexagesimale patru cifre, care este de 8 numere zecimale:

O altă aproximare timpurie a acestui număr în textul matematic vechi Shulba Sutra (... aprox 800-200 î.Hr.) este dată după cum urmează:

algoritmi de calcul

Există mai mulți algoritmi de calcul rădăcina pătrată a doua. Ca rezultat al algoritmului este obținut ca o valoare aproximativă ordinare sau zecimal. Cel mai popular algoritm pentru acest lucru, care este folosit în multe calculatoare și calculatoare, este metoda de calcul babilonian rădăcini pătrate. Acesta constă în următoarele:

Cele mai multe repetari în algoritmul (adică, mai mare decât «n»), cu atât mai bine apropierea rădăcinii pătrate a doua. Fiecare repetare dublează aproximativ numărul de cifre corecte. Iată câteva dintre primă aproximație:

Proprietățile rădăcinii pătrate a două

Jumătate √2 aproximativ 0.70710 67811 86548; această valoare conferă în coordonate geometria și trigonometria ale vectorului unitate, un unghi de 45 ° cu axele de coordonate:

Una dintre cele mai interesante proprietăți ale √2 este după cum urmează:

Acest lucru se datorează proprietăților secțiunii de argint.

O altă caracteristică interesantă a √2:

Rădăcina pătrată a doua poate fi exprimată în unitatea imaginară i folosind doar rădăcinile pătrate și operații aritmetice:

Rădăcina pătrată a 2 este singurul număr diferit de 1, a cărui tetracen egal cu pătrat sale fără sfârșit.

Rădăcina pătrată a doua poate fi de asemenea utilizat pentru a π aproximative:

Din punct de vedere al algebră mai mare. Este rădăcina polinomului, și, prin urmare, este un întreg algebric. O multitudine de numere de forma în care - numerele raționale. formează un câmp algebrică. Este de notat și este un subdomeniu al Reali.

Dovada iraționalității

Aplicam dovezile contrare. de exemplu, rațională. care este reprezentat ca o fracție ireductibilă, și unde - întregi. Vozvedom presupusa egalitate în pătrat:

.

Rezultă că, chiar și atunci, și este chiar. Să, în cazul în care întreg. atunci

Prin urmare, chiar și atunci, și este chiar. Am înțeles și chiar, contrar unei fracții ireductibile. Deci, ipoteza inițială a fost greșit, și - un număr irațional.

fracție continuă

Rădăcina pătrată a doua poate fi reprezentat ca o fracțiune a continuat:

fracțiunile adecvate ale fracției continuă dă valori aproximative converg rapid la exact rădăcina pătrată a doua. Metoda de calcul este simplu: dacă eticheta fracțiune adecvată anterior, ulterior are formă. Rata de convergență este mai mică decât cea a metodei lui Newton, dar este mult mai ușor de calculat. Am scrie primele câteva aproximări:

pătrat final este fracție (în cifre rotunde) 2.000000177.

dimensiunea hârtiei

Rădăcina pătrată a doua este proporția ISO 216. Raportul dimensiunii hârtiei Aspect este de așa natură încât la tăierea foii în jumătate paralel cu latura scurtă a celor două foi sunt obținute în aceeași proporție.

Vezi ce „rădăcina pătrată a 2“, în alte dicționare:

rădăcină pătrată din 3 - numere iraționale γ ζ (3) √2 √3 √5 φ α e π δ radix sistem numeric calificare √3 binar zecimal 1.7320508075688772935 1.1011101101100111101 ... ... ... Wikipedia

rădăcină pătrată din 5 - numere iraționale γ ζ (3) √2 √3 √5 φ α e π δ radix sistem Număr calificare √5 binar zecimal 2.23606797749978969 10.0011110001101111 ... ... ... hexazecimală Wikipedia

Rădăcină pătrată - Acest termen, există alte utilizări, a se vedea Root (dezambiguizare) .. Rădăcina pătrată a (rădăcina de gradul 2-a) este o soluție de forma ecuației. Cel mai adesea se referă la numărul de mai jos și, în unele aplicații, acestea pot fi, și alte ... ... Wikipedia

Rapid inversă rădăcină pătrată - Calcul iluminare și reflecție (ilustrat de first-person shooter-ul OpenArena) utilizează codul invers rapid rădăcina pătrată pentru a calcula unghiurile de incidență și de reflexie. inversă rapidă rădăcină pătrată (numit uneori rapid ... ... Wikipedia

Rapid inversă rădăcină pătrată - Calcul iluminare și reflecție (ilustrat de first-person shooter-ul OpenArena) folosește rădăcina pătrată de cod rapid invers pentru a calcula unghiurile de incidență și de reflecție ... Wikipedia

ROOT SQUARE - rădăcina pătrată a numărului, notată cu x, care, multiplicată cu ea însăși numărul x. Rădăcină pătrată din 4 este 2, prin urmare, TS4 = 2; C2 = 1.4142 (până la patru zecimale). Numerele negative sunt ... ... Știință și Tehnologie dicționar enciclopedic

rădăcină pătrată - rădăcina pătrată (rădăcina de gradul 2-a) este o soluție de forma ecuației. În ciuda faptului că în primul rând se referă la numărul de mai jos și în diferite considerații pot fi obiecte matematice ale naturii diferite, inclusiv, cum ar fi ... Wikipedia

ROOT - 1. În matematică - orice număr care, atunci când înmulțit cu el însuși numărul dat de ori dă acest rezultat; de exemplu, 2 - al doilea (sau pătrat) rădăcina 4, a treia (sau cubică) rădăcină 8 al patrulea rădăcină de 16, etc. 2. În lingvistică - ... Dicționar de Psihologie

ROOT - ROOT, rădăcină, pl. rădăcini, rădăcini, m. 1. îngropat în partea sol a plantei, prin Rui ea suge sucurile din sol. Eversion copaci furtună cu rădăcini. Stejar luate adânc rădăcini în pământ. || Lemn sau conținutul acestei părți a plantei. Lemn dulce ... Ushakov Dictionarul explicativ

rădăcină - substantiv. m. upotr. Comp. de multe ori Morfologie: (nu) ce? rădăcină, ce? rădăcină (a se vedea) ce? rădăcină, ce? rădăcină, ce? rădăcinii și mugurul; pl. ce? rădăcini (nu) ce? rădăcini, ce? rădăcini (vezi) ce? rădăcini, ce? rădăcini, ce? 1. Rădăcina rădăcinile acestei ... Explicativ dicționar Dmitrieva