procesare 6 matrice pascal
În acest caz, matricele a și b au 10 rânduri și coloane 30, și pe matrice,
în care există 16 rânduri și 14 coloane.
Pentru a accesa elementul de matrice trebuie să specifice denumirea în paranteze pătrate, separate prin virgulă rând și numărul coloanei:
Nume [LineNumber. column_num]
nume [LineNumber] [column_num]
De exemplu, h [2.4] 1 matricea elementului h. Este în conformitate cu numărul de
două și numărul coloanei patru.
Pentru a trata toate elementele matricei trebuie să fie utilizate două cicluri. Dacă matricea este procesată linie cu linie, în iterațiile buclei exterioare prin linia de la început până la sfârșit, atunci toate interior (primul, al doilea, al treilea și așa mai departe. D.) Elementele rândul curent. La prelucrarea elementelor matricei prin coloane exterioare ciclu buclă va trece prin coloane, șirul interior. Fig. 6.1 prezintă o schemă logică de prelucrare a rândurilor matricei în Fig. 6.2 coloane. Aici, numărul i rând, indicele coloana j, N numărul de rânduri, numărul M de coloane din matricea A.
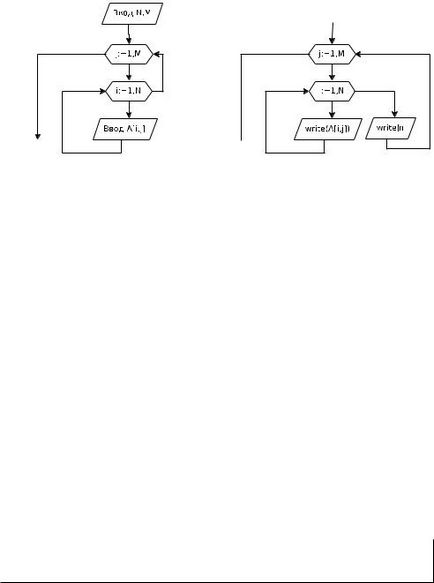
Algoritm elemente de matrice de ieșire progresivă este prezentată în Fig. 6.4.
Pe descrierea matrițele Pascal a fost descris în secțiunea 5.2 Capitolul 5. apel la elementul A i, j al matricei poate fi realizată prin structura c
Luați în considerare punerea în aplicare a matricelor de intrare-ieșire în aplicații consolă. Pentru organizarea matricei de intrare progresiv într-o buclă dublă în linii
și coloane, puteți utiliza operatorul citit.
pentru i: = 1 la N face pentru j: = 1 la m citesc; (A [i j.])
În acest caz, elementele de matrice ale fiecărui rând pot fi separate printr-un spațiu sau tab caractere și numai la sfârșitul liniei să apăsați Enter.

OBIECTIV 6.1. Scrieți o aplicație consolă de intrare matrice de numere reale și de ieșire-l pe ecranul monitorului.
Mai jos este o intrare-ieșire matrice aplicație consolă exemplu.
Introduceți matricea poate fi, de asemenea, organizate cu ajutorul următorului ciclu.
pentru i: = 1 la N face pentru j: = 1 m nu înceapă
scrie ( 'A (' i j ') =' .. .. ''); readln (A [i. j])
Pentru matrici de intrare-ieșire se pot utiliza componente de tip TStringGrid,
cu care ne-am întâlnit în capitolul 5.
Luați în considerare următoarea problemă ca un exemplu.
OBIECTIV 6.2. Crearea 2 program de matrice transpunere A.
transpunere matrice organigrame prezentată în Fig. 6.6. Atunci când matricea de transpunere A (N, M) este o matrice B (M, N).
Fig. 6.6. transpusa Flowchart matricea A
Să considerăm cazul particular de o dimensiune fixă de transpunere matrice A (4,3).
Pe forma și plasa o etichetă Label1 Label2 Legendă proprietățile unei matrice dat A și matricea transpusa B, TStringGrid două componente de tip. schimbarea proprietăților lor așa cum se arată în tabelul. 6.1. buton și transpus
formularul de cerere Fereastra prezentată în Fig. 6.7.
2 matrice transpusă matricei obținută din matricea originală (N, M), înlocuind rânduri în coloane.

Tabelul 6.1. Proprietăți StringGrid1 componente. StringGrid2.
// Adresa elementelor matricei are loc în coloane.
StringGrid2. C e l l s [i. j]: = IntToStr (B [j i].); se încheie;
Rezultatele programului sunt prezentate în Fig. 6.8.
Fig. 6.8. Rezultatele matricei programului de lucru transpunere A (3,4)
Pentru a demonstra matricea de intrare-ieșire prin intermediul unui tip de componentă TStringGrid am examinat lucrul cu matrici de dimensiuni fixe A (4,3) și B (3,4). Acum considerăm cazul general de rezolvare a problemei matricei transpunere A (N, M).
Punem următoarele componente pe forma:
• Label1 etichetă etichetat dimensiune ¾Vvedite matritsy¿;
• Eticheta label2 etichetate ¾ N = ¿;
• Eticheta label3 etichetate ¾ M = ¿;
• Eticheta label4 etichetată ¾Iskhodnaya matricea A ¿;
• Eticheta label5 etichetată ¾Preobrazovannaya matricea B ¿;
• câmp de intrare edit1 pentru introducerea numărului N;
• câmp de intrare Edit2 pentru introducerea numărului M;
• componenta StringGrid1 pentru intrare matricea inițială;
• Componenta StringGrid2 pentru stocarea matricei B transpuse;
• Cu ¾Vvod¿ butonul Button1 pentru a intra dimensiunile matricei etichetați;
• Butonul Button2 marcat ¾Ochistit¿ pentru a clarifica MAT
• Butonul Button3 etichetat ¾ ¿Transpunerea pentru rezolvarea problemei transpunerii matricei A;
• Butonul Button4 cu inscripția de ¾Vyhod programmy¿ pentru a finaliza
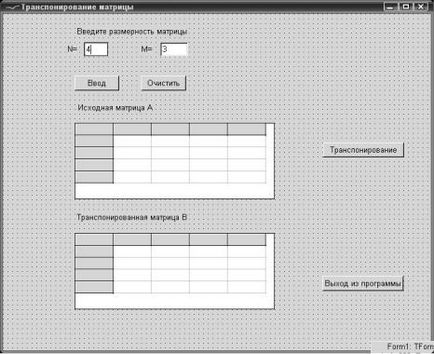
Puteți plasa componente pe un formular așa cum este prezentat în Fig. 6.9.
Fig. 6.9. Fereastra formă problemă de decizie matricea A transpusa (N, M)

Fig. 6.10. Începe ecranul programului de transpunere matrice A (N, M)
Proprietăți Set apar (vizibil) la False de componentele label4 etichete
label5. StringGrid1. StringGrid2. Button2 și Button3 butonul. Apoi, când
lansarea programului va fi doar componentele vizibile responsabile pentru dimensiunea matricei de intrare, și un program de buton (vezi. Fig. 6.10) 3 matrici A și B. N. M dimensiunile acestora vor declara în întreaga lume.
TForm1 = c l a s s (TForm)
Button1. TButton; Button2. TButton;
Button4. TButton; Edit1. tEditează;
proprietate Legendă 3 este setat pentru a forma matricea este transpusă.

StringGrid2. TStringGrid; privat
A, B: array [1. 2 5. 1 May 2] din întreg;
N, M: integer; Form1. TForm1;
software-ul buton de ieșire handler este standard și este prezentat mai jos.
Procedura TForm1. Button4Click (Sender TObject.); începe
Acum scrie butoanele de intrare handler care trebuie administrate și verifică corectitudinea dimensiunii matricei de administrare și setați proprietățile componentelor StringGrid1 StringGrid2 (numărul de rânduri și coloane) fac component StringGrid1 vizibile. Butonul Transpune, componente invizibile responsabile de intrarea dimensiunii matricei (eticheta Label1. Label2. label3. câmpurile de intrare edit1 și Edit2. butonul Enter).
Procedura TForm1. Button1Click (Sender TObject.); i var. octet; kod_n, kod_m, kod. întreg;
// Introduceti dimensiunea matricei.
// Informația de caractere este convertit într-un număr și stocat în //
Val (edit1 Text, N, kod_m.); // variabila M Val (Edit2 Text, M, kod_n.); // și N. variabile
// Dacă conversia a fost de succes și mărimea impunătoare // se potrivesc descrierii

i f (kod_n = 0) și (kod_m = 0) și (N> 0) și (N<26) and (M>0) și (M<26)
// redă prima matrice,
// Adresa elementelor matricei are loc în coloane.
StringGrid2. C e l l s [i. j]: = IntToStr (B [j i].); Buuton1. V i s i b l e: = False;
Rămâne să scrie handler eveniment atunci când faceți clic pe butonul Clear. Când faceți clic pe acest buton, trebuie să apară următoarele:
• conținutul componentelor de curățare StringGrid1. StringGrid2;
• Componente StringGrid1. StringGrid2 și etichetele lor corespunzătoare labe4 și label5. transpuna Butoanele sunt clare nevi-
• Butonul Enter devine vizibil;
• în câmpurile de intrare sunt scrise valorile inițiale ale dimensiunii matricei (N = 4,
Procedura TForm1. Button3Click (Sender TObject.); i var. j. întreg;
// componenta Clear StringGrid1. cu StringGrid1 do
pentru i: = 1 la ROWCOUNT - 1 do

pentru j: = 1 până la ColCount - 1 do
// componenta Clear StringGrid2. cu StringGrid2 do
pentru i: = 1 la ROWCOUNT - 1 face pentru j: = 1 până la ColCount - 1 do
// Asigurați componentele invizibile StringGrid1, StringGrid2, // labe4, label5.
StringGrid1. V i s i b l e: = False;
StringGrid2. V i s i b l e: = False; l a b e l 4. V i s i b l e: = False;
l o b e l 5. V i s i b l e: = False;
// Nu butoanele invizibile și ¾Transponirovat¿ ¾Ochistit¿.
Button2. V i s i b l e: = False;
Button3. V i s i b l e: = False;
// Marca buton vizibil ¾Vvod¿.
Button1. V i s i b l e: = True;
// înregistrează mărimea inițială a matricei // (N = 4. M = 3).
Edit2. Text: = '3'; se încheie;
Avem un program de lucru pentru transpunerea matricei. Fig. 6.11 prezintă rezultatele matricei transpunere A (2,4).
Notă utilizarea conexiunii cu numele componentei operatorului face declarație;
care facilitează accesul la proprietățile componentelor. Cu numele operatorului în termen
componente pentru a avea acces la proprietățile sale, nu se poate utiliza. De exemplu, pentru elementele de curățare a matricei A în loc de operatori