Prezentarea „volumul unei prisme drepte“
prezentarea Related
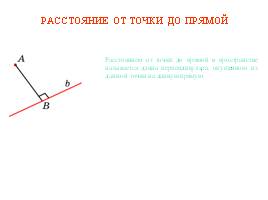





Slide-uri și textul acestei prezentări

Volumul unei prisme drepte
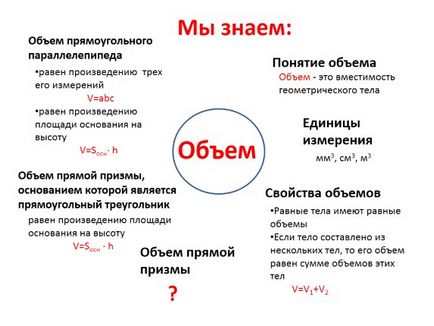
volum
Conceptul de volum
unități de măsură
volume egale ale corpului sunt egale în cazul în care organismul este compus din mai multe corpuri, volumul său este egal cu suma volumelor acestor corpuri V = V1 + V2
este egală cu produsul dintre cele trei dimensiuni V = abc este egală cu produsul dintre suprafața de bază la o înălțime de V = Sosn · h
este egală cu suprafața de bază a produsului la înălțimea V = Sosn · h
Volumul unei prisme drepte
?
Volum - Această capacitate corp geometric
volume proprietăți
Volumul unei prisme drepte a cărei bază este un triunghi dreptunghiular
Volumul unui paralelipiped
mm3 cm3 m3
Știm:
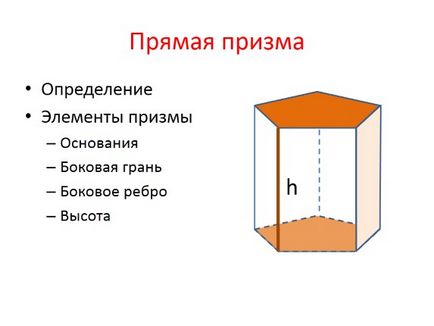
prisme drepte
Definirea elementelor Bazele prismei feței laterale înălțimea nervurii laterală

supoziție
produsul din înălțimea zonei de bază
Deplasarea este o prismă drept.
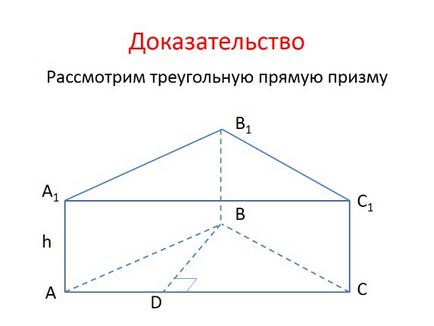
Luați în considerare prisma triunghiulară
evidență
D
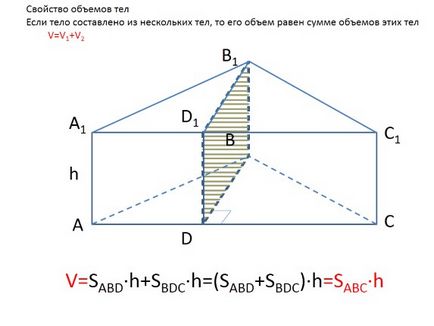
V = SABD · h + SBDC · h = (SABD + SBDC) · h = SABC · h
Volumele de proprietate a corpului în cazul în care organismul este compus din mai multe corpuri, volumul său este egal cu suma volumelor acestor corpuri V = V1 + V2
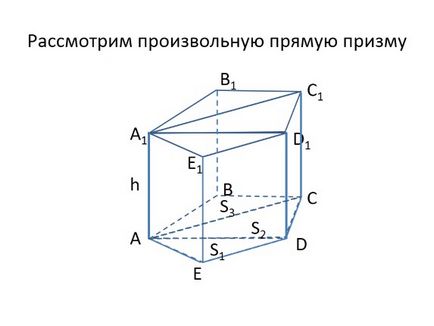
Luați în considerare o prismă
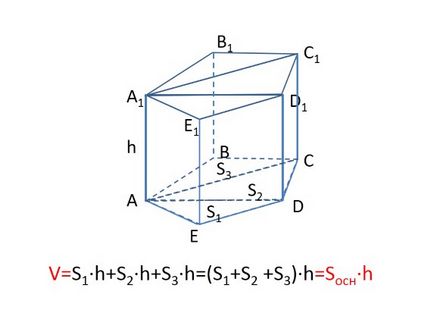

Un volum prismă dreapta este produsul de bază pătrată și înălțimea
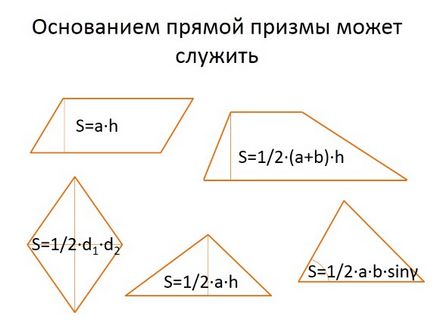
Motivul poate fi o prismă drept
S = 1/2 · o · h
S = 1/2 · (a + b) · h
S = 1/2 · d1 · d2
S = a · h
S = 1/2 · a · b · sinγ
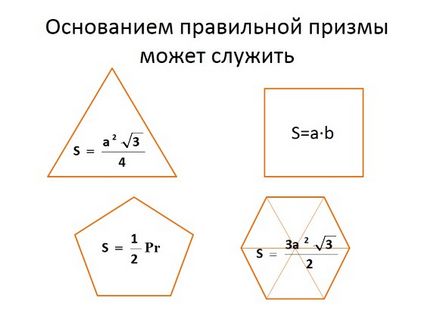
Motivul poate fi o prismă corectă
S = a · b
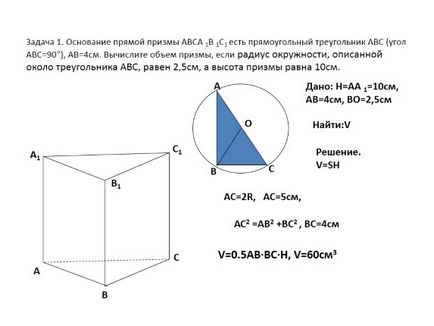
Problema 1. Baza dreapta prism ABCA 1C1 1B este triunghi dreptunghiular (unghi ABC = 90 °) ABC, AB = 4cm. Se calculează volumul prismei dacă raza cercului circumscris triunghiului ABC este egală cu 2,5 cm, iar înălțimea prismei este 10cm.
despre
A
C
A1
B1
C1
A
C
oh
Aceasta este dată de: H = AA 1 = 10cm, AB = 4cm, VO = 2,5cm
Cauta: V
Decizie. V = SH
AC = 2R, AC = 5cm,
AC2 = AB2 + BC2. BC = 4cm
V = 0.5AB ∙ BC ∙ H, V = 60sm3
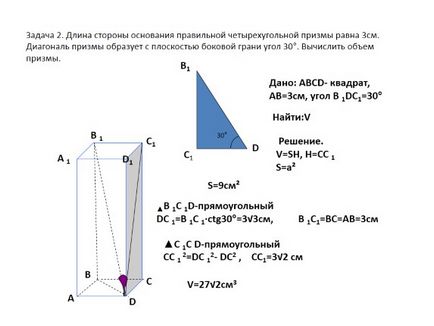
Problema 2. Lungimea bazei prismei este patrulateră regulată 3cm. forme de prisme diagonale cu planul unghiului față laterală 30 °. Calculați volumul prismei.
A
C
D
A 1
B 1
C1
D1
C1
B1
D
30 °
Dată: pătrat AVSD- AB = 3cm, unghiul B este de 30 ° 1DC1 =
Cauta: V
Decizie. V = SH, H = SS 1 S = a²
S = 9cm²
▲ La 1C 1D-rectangular DC 1 = B 1C 1 ∙ ctg30 ° = 3√3sm, B 1C1 = AB = BC = 3cm
▲ C 1C D dreptunghiulare CC luna februarie 1 = DC 12- DC2. CC1 = 3√2 cm
V = 27√2sm3
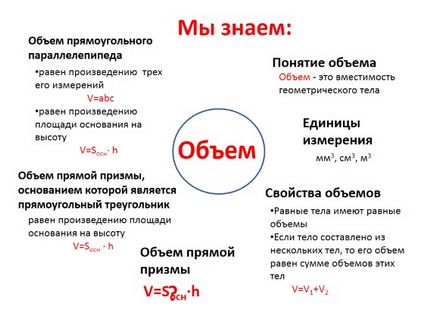
volum
Conceptul de volum
unități de măsură
volume egale ale corpului sunt egale în cazul în care organismul este compus din mai multe corpuri, volumul său este egal cu suma volumelor acestor corpuri V = V1 + V2
este egală cu produsul dintre cele trei dimensiuni V = abc este egală cu produsul dintre suprafața de bază la o înălțime de V = Sosn · h
este egală cu suprafața de bază a produsului la înălțimea V = Sosn · h
Volumul unei prisme drepte
?
Volum - Această capacitate corp geometric
volume proprietăți
Volumul unei prisme drepte a cărei bază este un triunghi dreptunghiular
Volumul unui paralelipiped
mm3 cm3 m3
Știm:
V = Sosn · h

teme pentru acasă
Teorema pp. 145 663 Baseline № Nivel avansat № 659
Mult noroc pentru tine!

Ppezentatsiyu preparat Vakilova VV profesor de matematică KOGOAU „Multidisciplinară Liceul g.Vyatskie Polyana“

Cărți folosite:
L.S.Atanasyan Geometrie 10-11 Internet resursy- de diapozitive 12, 13