Pregătirea studenților pentru examenul și OGE (DPA), în rezoluția centru de formare (manual de matematică -
transforma avionul
Definiție 1. Transformarea avionului se numește o regulă. prin care fiecare punct al planului nu corespunde unui punct al aceluiași plan.
Definirea 1 implică faptul că, în cazul F - transformarea planului a. și M - un punct arbitrar al avionului. F (M) este, de asemenea, un punct al planului a.
2. Determinarea punctului F (M) a numit punctul de imagine M atunci când conversia unui punct M F. prototip numit F (M), la punctul de conversie F.
Sunt definite în mod similar și inverse imagini de orice piese pe planul de transformare F.
3. Determinarea Transformă plan numit plan de transformare bijectivă în sine. în cazul în care diferitele puncte au diferite imagini. și fiecare punct este planul imaginii inversă.
Cu alte cuvinte, atunci când o transformare unu-la-unu a planului pe diferite puncte ale planului se deplasează în diferite părți ale aceluiași plan, și în fiecare punct al planului trece un anumit punct al acestui plan.
DEFINIȚIE 4. Produsul (compoziția) a două transformări se numește transformare, care este obținut prin realizarea secvențială aceste transformări.
Astfel, în cazul în care F și G - două conversii, produsul acestor transformări va fi o transformare a H, A este un punct arbitrar într-un plan trebuie să punctul A „a acestui plan, definit de formula:
planul de mișcare
DEFINIȚIE 5. avionul Mișcarea se numește un plan de transformare, în care distanța dintre oricare două puncte din planul este egală cu distanța dintre imaginile lor.
Următoarele transformări sunt mișcări plane:
1. transferul paralel (deplasare) a unui vector predeterminat
In planul de transport paralel cu un vector predeterminat (Fig.1) Un plan al unui punct arbitrar merge într-un plan Un punct“ca egalitatea
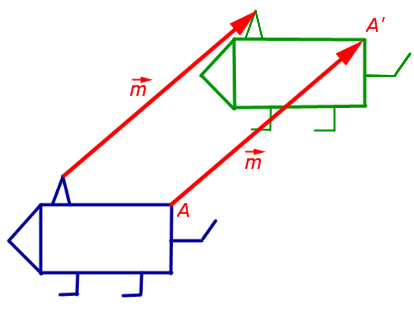
Notă. Mișcarea, în care fiecare punct al planului rămâne în loc, numit transformarea identității. Transformarea identitate poate fi privită ca o translație paralelă pe un vector egal cu zero.
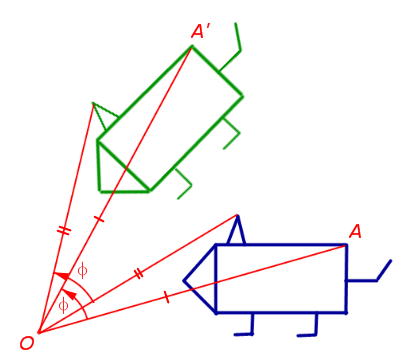
2. Rotirea în jurul punctului specific numit centrul de rotație la un unghi predeterminat
Prin rotirea în jurul planului punctul O cu un unghi φ (fig. 2), fie un punct arbitrar A în planul trece un avion punct A“, că egalitati
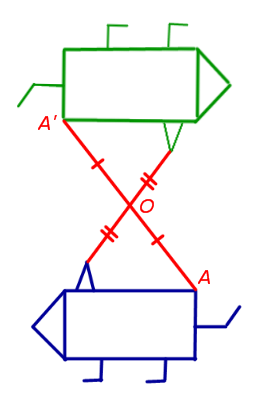
3. Simetria centrală (simetrie în raport cu un punct predeterminat numit centru de simetrie)
În planul central de simetrie în raport cu punctul O să fie un punct arbitrar A în planul trece de un punct A „planul ca punctul median al AA segment“ este punctul O - centrul de simetrie predeterminat (Figura 3).
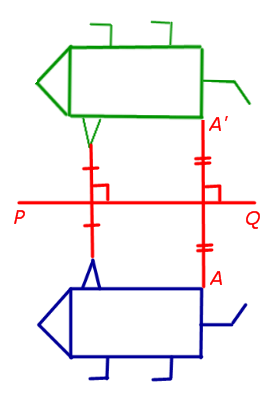
4. axial simetrie (simetrie în raport cu linia dată, numita axa de simetrie)
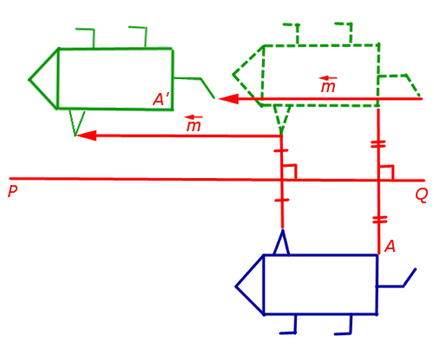
Când simetrie axială în raport cu o linie dreaptă PQ (axa de simetrie) al unui punct arbitrar A în planul trece de un punct A „planul, că, în primul rând, linia AA“ perpendicular pe linia PQ. și, în al doilea rând, punctul de intersecție al liniilor AA „și PQ este punctul de mijloc al AA“
5. simetrie glisant (compoziție simetrie axială față de linia dată și transferul paralel al unui predeterminat vector nenul paralel cu această linie dreaptă)
Dacă linia PQ - axa de simetrie și vectorul de translație paralelă este dată de o linie paralelă PQ. în mișcare rezultatul simetrie poate fi reprezentat în mod convențional după cum urmează, așa cum se arată în figura 5.
Propunerea de orientare plan de conservare. plan de mișcare schimbare de orientare. teorema Sala
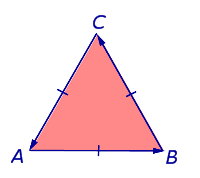
Luați în considerare pentru un triunghi echilateral plan arbitrar, iar literele reprezintă nodurile A, B și C, astfel încât să meargă de-a lungul laturilor triunghiului în direcția
triunghi sunt dispuse pe stânga (Fig.6). Cu această notație vârfurile unui triunghi tur se va efectua invers acelor de ceasornic.
Să presupunem acum că o mișcare F ia triunghiul ABC în triunghiul A'B'C“, care
Din moment ce fiecare mișcare a planului păstrează distanța dintre punctele, triunghiul A'B'C „va, de asemenea, echilateral, cu toate acestea, următoarele două cazuri.
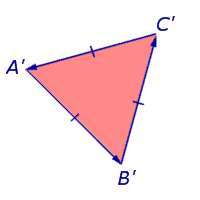
În primul caz, bypass-ul de pe părțile laterale ale triunghiului A'B'C „în direcția
Triunghiul A'B'C „este situat pe partea stângă. și by-pass se realizează în sens antiorar (Figura 7).
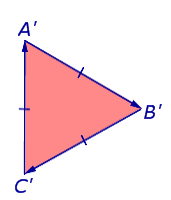
În al doilea caz, un circuit de-a lungul laturilor triunghiului A'B'C „direcție
Triunghiul A'B'C „este situat în partea dreaptă. și by-pass se realizează în sensul acelor de ceasornic (Figura 8).
Definiție 6. În cazul în care primul caz se realizează atunci când se deplasează F, atunci această mișcare este mișcarea care păstrează orientarea plan (mișcarea primul fel, mișcarea propriu-zis). Când F mișcare se efectuează al doilea caz, o astfel de mișcare se numește mișcare, schimbarea orientării (mișcare a două fel, mișcarea improprie).
Clasificarea tuturor mișcărilor avionului dă următoarea teoremă Sala.
Teorema lui Chasles. Orice orientare plan mișcare de conservare, sau o deplasare paralelă. sau de cotitură. Orice plan de mișcare schimbare de orientare, este sau simetrie axială. sau o reflecție alunecare.
plan de transformare afină
7. Determinarea planului de transformare afină se numește transformare plan unu-la-unu în sine, în care orice mod direct avionul este o linie dreaptă.
Deoarece fiecare plan de circulație poartă linii drepte în linii drepte, fiecare mișcare este o transformare afină.
Cu toate acestea, transformările afine nu sunt limitate la planul de mișcare. Următoarele transformări sunt, de asemenea, afin plan transformări:
1. Compression (întindere) la linia cu un raport de compresie predeterminat (expansiune)
În timpul compresiei (expansiune) a planului de la linia dreaptă PQ specifica raportul de compresie k (Fig.9) Un avion al unui punct arbitrar merge într-un plan Un punct“, că sunt îndeplinite următoarele condiții:
- AA directă „perpendicular pe linia PQ;
- dacă este marcat cu litera A „punctul de intersecție al liniilor AA„și PQ. nu va fi egalitate
| A'A "| = | k | | AA" | ;
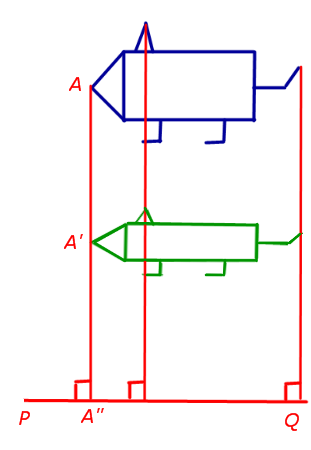
Notă 1. În cazul în care | k | <1. рассматриваемое аффинное преобразование называют сжатием к прямой PQ. если же | k |> 1. că această transformare se numește dilatarea.
Remarcă 2. Vom folosi pentru comprimarea dat (tensiune) desemnarea
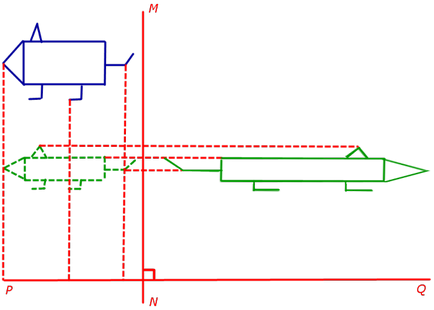
2. Compression (tracțiune) prin două direcții reciproc perpendiculare predeterminate cu compresie coeficienți predeterminate (expansiune)
Să PQ și MN - două linii drepte reciproc perpendiculare, iar k1 numerelor și k2 - rapoarte de compresie (extensie) plane în direcția liniilor de PQ și MN, respectiv. Apoi, compresia (expansiune) a lungul a două direcții reciproc perpendiculare specifica PQ și MN cu coeficienți k1 și k2 (fig.10) se numește compoziție compresiuni (neîntins).
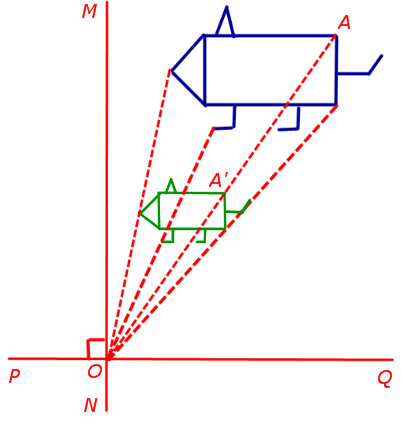
3. Omotetie cu un centru de homothetic predeterminat și specifica raportul de compresie (expansiune)
Homothety centrată la O și coeficientul k se numește transformare afină, în care un punct arbitrar A în planul trece de un punct Un avion“, că sunt îndeplinite următoarele condiții:
- punctul A „se află pe linia AO;
- egalitate
Notă. Luați în considerare două linii perpendiculare arbitrare PQ și MN, intersectându punctul O. Apoi homothety cu centrul la O și un coeficient k coincide cu compresie (expansiune) în direcțiile PQ și MN cu coeficienți egal cu k. Cu alte cuvinte, dilatarea este contracțiile compoziției (entorsă):
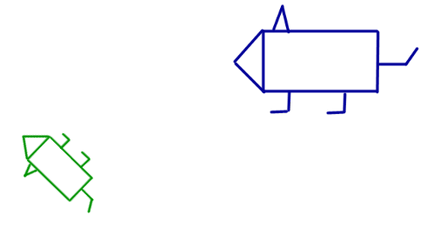
4. Transformarea similaritate cu un factor de scalare predeterminat
Transformarea Similaritatea cu k coeficient de similaritate numit transformare afină reprezentat printr-o compoziție cu coeficientul k homothetic și mișcarea (fig. 12).
Clasificarea transformărilor afine ale planului
Puteți obține, de asemenea, cunoștință cu profesorii dezvoltat un centru de formare „rezolutiv“ materiale de instruire pentru a se pregăti pentru examen și OGE (DPA), în matematică.
Pentru studenții care doresc să se pregătească bine și să treacă examenul sau OGE (DPA) în matematică, fizică sau limba română pentru un scor mare, centrul de formare „rezolutiv“ deține