Modelul nuclear al atomului - examinare, pagina 1
Modelul nuclear al atomului
Rutherford pe baza experimentului de împrăștiere
a-particule pe o folie metalică la pământ atomii de model planetar al structurii atomice.
Conform acestui model, atomul este format dintr-un nucleu greu încărcat pozitiv de dimensiuni foarte mici (
10-15 m), în jurul căreia electronii se deplasează de-a lungul unor orbite. Razele acestor orbite au dimensiuni
Prezența sarcinii electronului face ca modelul planetar al termenilor contradictorii ale fizicii clasice, din moment ce rotirea electronilor în jurul nucleului, ca orice particulă încărcată în mișcare rapidă trebuie să radieze unde electromagnetice. Spectrul aceste radiații trebuie să fie continuu. In experimentele observate atomii de radiație de spectru liniar. În plus, radiația continuă reduce energia electronului, iar aceasta se datorează reducerii orbitei ar fi trebuit să cadă în nucleu.
postulate Niels Bohr
Niels Bohr „salvat“ modelul planetar pentru un atom de hidrogen, formulând trei postulate.
1. Un electron dintr-un atom se poate deplasa doar în anumite orbite staționare cu un anumit număr n = 1; 2; 3; ... Mutarea pe orbită închisă fixă a electronului are o energie totală constantă En.
2. orbite staționare permise sunt numai acelea pentru care momentul cinetic al electronilor este egală cu o valoare multiplă integrală a lui Planck
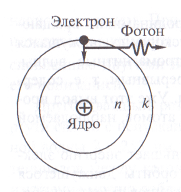
3. Emisia de fotoni sau absorbția are loc la atomul de tranziție de la o stare de echilibru în alta. Frecvența de radiații
Calculul atomului de hidrogen al Bohr
cei care - masa de electroni
Rezolvarea sistemului acestor două ecuații, obținem:
unde a = 0,529. 10-10 m - raza primei staționare
orbite ale atomului de hidrogen
Energia cinetică a electronului
Energia potențială a electronului
Energia totală din orbita p-lea
Frecvența radiației la trecerea de la o stare de a obține n
, în cazul în care - constanta Rydberg
Există, de asemenea, constanta Rydberg pentru λ ν și:
Pentru atomii de hidrogen (ion heliu A + Z = 2, dvuhkratno- litiu ionizata Li ++ c Z = 3, +++ trohkratnoionizovanny beriliu Be Z = 4, etc.) sunt razele orbitelor electronilor în timpurile Z mai mici decât un atom de hidrogen și un spectru de energie de hidrogen-ion este obținută prin multiplicarea cu Z2
Teoria cuantică a atomului
Desi teoria lui Bohr dă rezultate bune pentru atomi de hidrogen, aceasta nu poate fi considerată o teorie completă a fenomenelor atomice.
Din punct de vedere al fizicii moderne atom este un sistem fizic, care cu siguranță nu poate fi descrisă de teoria clasică, fără a lua în considerare proprietățile val de electroni care se deplasează în atomul ca lungimea de undă de Broglie a electronului este comparabil cu dimensiunile atomice.
Energia potențială de interacțiune a electronului cu nucleul atomului de hidrogen, cum ar fi
distanța r- dintre electroni și nucleu, care, în primă aproximație,
Vom fi privit ca un punct.
Propunerea de un electron într-un astfel de câmp poate fi privit ca mișcare într-un potențial sferic bine.
Spectrul energiilor electroni trebuie să fie discret, adică Se compune din niveluri individuale de energie cu
Valorile de energie totală E 1 a electronului; E 2; E 3, etc.
ecuația Schrödinger este
Soluția acestei ecuații se realizează în coordonate sferice r, θ, φ. al cărui centru coincide cu centrul nucleului atomului. Într-un astfel de sistem,
Folosind un moment unghiular operator de pătrat într-un sistem de coordonate sferic
ecuația Schrodinger sunt transformate în
Soluția acestei ecuații sunt în căutarea într-un produs de două funcții cu mai multe variabile
C, ținând cont de cerințele impuse naturale asupra funcției Ψ- trebuie să fie lipsită de ambiguitate, finită, continuă și netedă.
În procesul de rezolvare se constată că aceste cerințe pot fi satisfăcute pentru toate valorile pozitive ale energiei E, dar valorile negative ale E - numai la valori discrete, și anume în cazul în care
care corespunde stări legate de electroni într-un atom.
Astfel, rezultatele de soluție ecuația Schrodinger în cazul E 1 2 3 4 A se vedea toate