Lecția „axiome stereometrie“

Text Lecții de decodare:

Ce este o axiomă?

Axioma - această afirmație este de la sine înțeles.

Axiomele geometriei solide - declarații privind proprietățile solide geometrice, luate ca ipotezele pe care toate teoremele sunt dovedite și întreaga geometria este construită.

Axioma A1. Prin orice trei puncte care nu se află pe o linie dreaptă, trece un avion, și numai unul.

Axioma A1 este format din două părți.

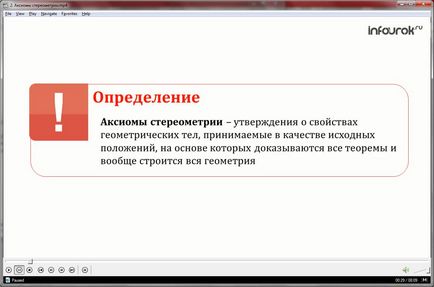
Prima parte a revendicărilor care trece prin trei puncte ale planului, adică există cel puțin un plan.

O a doua parte a axiomei spune că aceasta este doar un singur plan.

Ecranul descrie trei puncte A, B și C.

Dacă C nu aparține liniei AB, există α plan care trece prin aceste trei puncte, în care doar unul.

Simbolul este citit ca exista.

Conform acestei axiome, cele trei puncte, care nu se află pe o linie dreaptă, în mod unic determină un plan.

Prin urmare, planul este uneori referire la trei litere mari, folosind oricare dintre cele trei puncte ale planului care nu se află pe o linie dreaptă.

Am pe planul ecranului este desemnat ca α. Același plan poate fi desemnat ca ABC

Axioma A2. În cazul în care cele două puncte de pe linia de minciuna într-un plan, atunci toate punctele de minciuna linie în acest plan.

În acest caz, se spune că linia se află în planul sau planul trece prin linia.

Pe ecran vedeți două puncte A și B.

În cazul în care punctele A și B fac parte avionul. atunci linia dreaptă AB se află într-un plan α, trece prin planul liniei AB.

Această axiomă stabilește o relație între linia și planul, adică, faptul că avionul este într-adevăr plat și nu este o consecință directă „Înghiontelile“ și este conținută în ea.

Din Axioma A2 rezultă că în cazul în care linia nu se află în planul, atunci nu are mai mult de un punct în comun cu ea.

În cazul în care linia dreaptă și planul are un singur punct comun, atunci spunem că ele se intersectează.

În cazul în care două avioane au un punct comun, atunci ei au o linie comună pe care se află toate punctele comune ale acestor avioane.

În acest caz, se spune că avioanele se intersectează de-a lungul unei linii care trece prin acest punct ..

Pe ecran vom vedea planul au un punct comun M.

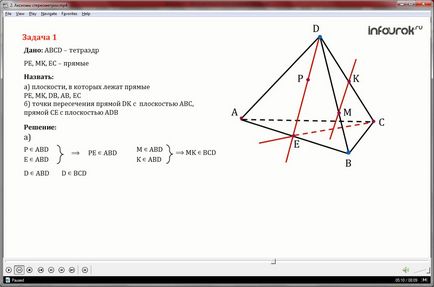
În cazul în care punctul M - totalul pentru avioane. ele se intersectează într-o linie dreaptă-o, care trece prin punctul M.

Această axiomă este foarte important. Ea susține că cele două planuri nu pot trece de la un singur punct.

fapte planimetrie Justiție

Suntem familiarizați cu cele trei axiome ale geometriei solide.

Întrebarea este: „Putem folosi faptele care sunt adevărate în avion: teorema lui Pitagora, zona formula de triunghiuri, paralelograme? Sau toate aceste formule, teoreme nu contează pentru noi? "

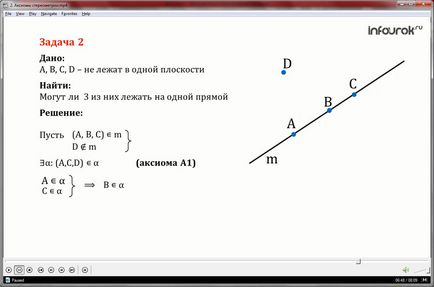
În planimetrie am fost de-a face cu un singur plan, care a găzduit toate cifrele care le-am considerat. Geometria solida in mai multe planuri.

Și în fiecare dintre avioanele sunt doar faptele de geometrie plana. În oricare dintre planurile se face teorema lui Pitagora pentru triunghiul din dreapta, circumferința cu formula adevărată, fidelă formulei pentru zona.

Tot ceea ce am studiat, putem acum în condiții de siguranță să fie utilizate în fiecare dintre planurile avute în vedere.