Lagrange metoda de multiplicare - studopediya

LP și NLP probleme sunt rezolvate în 1 pas. Asemenea probleme sunt numite-o singură etapă (același tip). Dean sarcină. Pr. numita mai multe etape - la fiecare pas este determinată de decizia unor părți ale sarcinilor cauzat problema inițială.

Formularea generală a obiectivelor DP. Lăsați un sistem fizic S este într-o stare inițială S0 Je Snach. și este ușor de gestionat. Datorită câteva exerciții fizice. U, sistemul trece de la starea inițială la starea finală S0 Skon. Skon Je SK.

Astfel, pe măsură ce fiecare dintre comenzile U este caracterizată prin valoarea corespunzătoare a funcției W (U).

Provocarea este de a găsi o multitudine de controale, în care funcția W (U) are o valoare extremă.

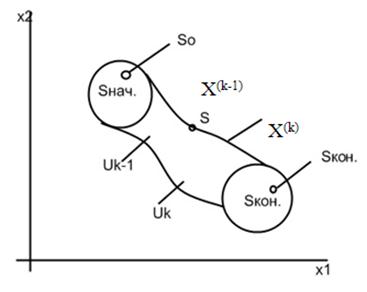
DP de rezolvare a problemelor se realizează în cadrul schemei:

Presupunem că starea sistemului S a considerat pe care k - m pas, cu k = 1 ... n determinat de o combinație de numere X (k) = (x1 (k) x2 (k) ... xn (k) ..), Care sunt derivate uk rezultat al sistemului de control oferă o tranziție Siz stare x (k-1) la starea x (k).

Se presupune că statul X (k) depinde de starea X (k-1) și controlul selectat Marea Britanie, dar nu depinde de modul în care sistemul S-a trecut în această stare.

Incizia. câștig de stat Pentru a pune în aplicare prima etapă a fost obținută depinde prev. stat (X (k-1)) și ecuația Uk.

Contribuția totală în acest caz va fi:

F = Σ Wk (X (k-1), Marea Britanie)

DP pentru rezolvarea problemelor de un astfel de sistem se realizează în conformitate cu principiul optimalității Bellmona.

Declaratie: ce ar fi fost starea sistemului înainte de etapa următoare ar trebui să fie următorul pas este de a alege controlul, astfel încât câștigul în această etapă, plus câștigul optim la toate etapele ulterioare a fost maximă.