Intervale de creștere și descreștere

Următoarele tipuri de funcții monotonia:

1) funktsiyavozrastaet. În cazul în care la un anumit interval, în cazul în care astfel încât este valabil pentru oricare două puncte, și acest interval de timp care. Ie valoare mai mare a argumentului corespunde unei valori mai mari a funcției;

2) funktsiyaubyvaet. În cazul în care la un anumit interval, în cazul în care astfel încât este valabil pentru oricare două puncte, și acest interval de timp care. Ie valoare mai mare a argumentului corespunde valorii minime a funcției;

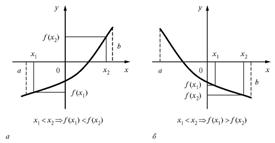
3) funktsiyaneubyvaet. În cazul în care la un anumit interval, în cazul în care astfel încât este valabil pentru oricare două puncte ale intervalului și că;

4) funktsiyanevozrastaet. În cazul în care la un anumit interval, în cazul în care astfel încât este valabil pentru oricare două puncte, și acest interval de timp care.

2. Pentru primele două cazuri, termenul „monotonie strictă“ se aplică în continuare.

3. Ultimele două cazuri sunt specifice și, în general, definit ca o compoziție a mai multor funcții.

4. Separat, observăm că ia în considerare creșterea și scăderea funcțiilor de program să fie exact la stânga la dreapta și nimic altceva.

Funcția se numește ciudat. dacă schimbați semnul argumentului, se schimbă valoarea sa opus. Formula arata ca acest post. Aceasta înseamnă că, după înlocuirea funcției în locul tuturor valorilor lui X „minus X“, funcția își schimbă semnul. Graficul acestei funcții este simetrică cu privire la originea.

Exemple sunt funcții impare, și altele.

De exemplu, graficul nu posedă simetrie cu privire la originea:

Funcția se numește chiar. în cazul în care semnul schimbării argument, aceasta nu se schimba valoarea sa. Formula arata ca acest post. Aceasta înseamnă că, după înlocuirea funcției în locul tuturor valorilor lui X „minus X“, funcția ca urmare nu se va schimba. Graficul acestei funcții este simetrică în jurul axei.

Exemple de funcții chiar sunt și colab.

De exemplu, grafica arată simetrie față de axa:

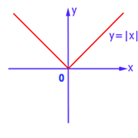
Dacă funcția nu aparține uneia dintre aceste tipuri, se numește fie o funcție de par sau impar sau generale de tip. Astfel de funcții nu au nici o simetrie.

Această funcție, de exemplu, este unul recent, am examinat o funcție liniară a programului:

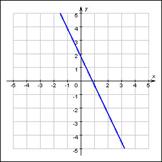
3. Proprietățile speciale ale funcțiilor este frecvența.

Faptul că periodicitatea funcției, care sunt considerate a curriculum-ului standard, sunt doar funcții trigonometrice. Am vorbit deja în detaliu despre ele în studiul subiectelor relevante.

Periodicitatea funcției - o funcție care nu se schimba valoarea prin adăugarea la argumentul unui anumit număr de constante non-zero.

Acest număr minim se numește perioada funcției și este notată cu litera.

Formula acestei înregistrări este după cum urmează :.

Să ne uităm la un exemplu de această proprietate pe un grafic sine:

Să ne amintim că perioada funcțiilor este. și perioada și -.

După cum știm deja, pentru funcțiile trigonometrice cu un argument complex, poate fi o perioadă de non-standard. Este vorba despre funcțiile de forma:

Ei au o perioadă egală cu. Și despre funcțiile:

Ei au o perioadă egală cu.

După cum puteți vedea, pentru calcularea unei noi perioade, o perioadă de standard se împarte la factorul pentru argumentul. Din celelalte modificări funcție nu depinde.

O funcție y = f (x) se numește mărginită de dedesubt de un H⊂D set (f), în cazul în care există un număr și că pentru orice x # 1013; x satisface inegalitatea f (x)

O funcție y = f (x) se numește o limită superioară de pe H⊂D set (f), în cazul în care există un număr și că pentru orice x # 1013; x satisface inegalitatea f (x)

În cazul în care X nu este specificat un interval, se consideră că funcția este mărginită pe domeniul său. Funcționalitate limitată, și de mai sus și mai jos se numește mărginită.

Limitări ale funcției este ușor de citit pe program. Puteți desena o anumită linie y = a, iar în cazul în care funcția este mai presus de această linie, apoi delimitată de mai jos.

Dacă inferior, respectiv, de sus. Mai jos este un grafic de mai jos funcție mărginită. Programeaza o funcție limitată, băieți, încearcă să se picteze.

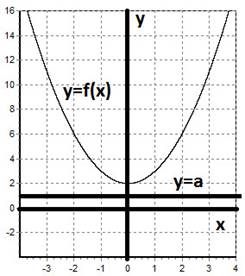
Subiect: Proprietățile funcțiilor: intervale de creștere și descreștere; valorile maxime și minime; punctul extremum (maxim local sau minim), funcția de convexitate.

Intervale de creștere și descreștere.

Bazat condiții suficiente (atribute) ale creștere și descreștere funcții sunt intervale de creștere și descreștere funcții.

Iată formularea semnelor de creștere și scăderea funcției în intervalul:

· Dacă derivata funcției y = f (x) este pozitiv pentru toate x din creșterile intervalului funcției X. prin X;

· Dacă derivata funcției y = f (x) este negativă pentru toate x din X. Funcția interval scade la X.

Astfel, pentru a determina intervalele de creștere și descreștere funcție ar trebui:

· Găsiți domeniul funcției;

· Găsiți derivata funcției;

· Rezolva inegalitățile și domeniu;

· Adaugă la lacunele care rezultă punctul limită în care funcția este definită și continuă.

Luați în considerare exemplul unei constatări de creștere a intervalelor și scăderea funcției pentru a explica algoritmul.

Găsiți intervale de creștere și scădere a funcției.

În primul pas trebuie să găsiți domeniul funcției. În exemplul nostru, expresia în numitorul nu devine nulă, prin urmare.

Ne întoarcem la găsirea derivata unei funcții:

Pentru a determina intervalele de creștere și descreștere, pe o bază suficientă pentru a rezolva funcție de inegalitățile și domeniu. Noi folosim o generalizare a metodei intervalului. Singurele rădăcini reale ale numărătorului este x = 2. iar numitorul devine zero la x = 0. Aceste puncte împart domeniului în intervale în care derivatul păstrează semn. Notă aceste puncte pe o linie de număr. De cotloanele denota convențional intervale pentru care derivatul este pozitiv sau negativ. Săgețile indică mai jos schematic crește sau descrește funcția la intervalul corespunzător.

Astfel, ambele.

La punctul x = 2, funcția este definită și continuă, cu toate acestea trebuie adăugat la diferența de a crește și descrește decalajul. La punctul x = 0 nu este definit, prin urmare, nu include acest punct, în intervalele dorite.

Aici este funcția program pentru comparație cu ei rezultatele.

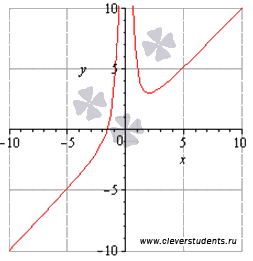
A: Funcția este în creștere la. scade în intervalul (0, 2].