identități trigonometrice de bază, producția de formulele

În acest articol, vom lua în considerare pe deplin identitatea trigonometrice de bază. identitățile trigonometrice de bază sunt egale, stabilirea unei conexiuni între sinus, cosinus, tangenta și cotangentă unghiului și se lasă să găsească oricare dintre cele cunoscute funcții trigonometrice printr-o alta.

Imediat lista identitățile trigonometrice de bază, care analizează în acest articol. Scrieți-le în tabelul de mai jos da o derivare a acestor formule și să dea explicația necesară.

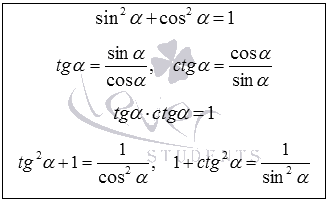
Navigare în pagină.

Legătura dintre sinusul și cosinusul unghiului

Aceasta este, de interes deosebit este egalitate, care a dat numele identitățile trigonometrice de bază.

Înainte de a dovedi identitatea trigonometric pitagoreic, da formulare: suma pătratelor sinusul și cosinusul unghiului este identic egal cu unu. Acum dovedesc.

Referindu-se la cercul unitate. Să presupunem că punctul de pornire A (1, 0), după rotirea printr-un unghi în punctul A1. Prin definițiile sinus și cosinus a punctului A1 are coordonatele. Mai mult, A1 se află pe cercul unitate, de aceea, coordonatele trebuie să îndeplinească cercul unitate, care are forma x 2 + y 2 = 1. Adică, ar trebui să existe egalitate. Acest lucru dovedește identitatea trigonometrice pitagoreice pentru toate unghiurile de rotație.

Egalitatea este adesea numit teorema lui Pitagora în trigonometrie. Să ilustrăm acest punct.

Ia cercul unitate. Rotiți punctul de pornire A (1, 0), în jurul unui punct O cu un unghi. Lăsați punctul A după rotație devine punctul A1 (x, y). Picătură de la punctul A1 A1 H perpendicular pe linia Ox.

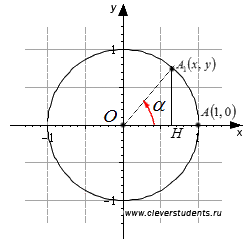
Luați în considerare triunghiul dreptunghiular OA1 H. văzut clar în ea că lungimea picioarelor A1 H și OH sunt, respectiv abscisei și ordonata punctului modulul A1. adică | A1 H | = | y | și | OH | = | x |. OA1 și lungimea ipotenuzei este egală cu raza unei unități cerc, adică | OA1 | = 1. Teorema lui Pitagora ne permite să scrie egalitatea | A1 H | 2 + | OH | 2 = | OA1 | 2. putem fi rescrisă ca | y | 2 + | x | 2 = 1 sau 2 y 2 + x 2 = 1. Dar, prin definiție, și apoi din ecuația y 2 + x 2 = 1, putem muta spre egalitate.

Identitatea trigonometrice pitagoreice este adesea folosit la conversia expresii trigonometrice. Aceasta permite suma pătratelor sinusul și cosinusul unghiului unității înlocuit. Cel puțin o parte a identității trigonometrice de bază este utilizată în ordine inversă: unitatea este înlocuită cu suma pătratelor sinus și cosinus unui unghi.

Tangentă și cotangentă prin sinus și cosinus

Identități de conectare tangentă și cotangentă cu sinus și cosinus a unghiului de un fel și imediat urmați definițiile sinus, cosinus, tangentă și cotangentă. Într-adevăr, prin definiție, are ordonata y sinus, cosinus este abscisă x, tangenta este raportul dintre ordonata la abscisă, adică, un pat de copii este raportul dintre abscisa de ordonata, adică.

Datorită acestei identități evidente și de a determina de multe ori tangenta și cotangentă dată nu de raportul dintre abscisa și ordonata, și un raport de sinus și cosinus. Deci, tangenta unui unghi este raportul dintre sinusul la cosinusul unghiului, și cotangentă - raportul dintre sinusul la cosinusul.

Pentru a încheia această secțiune trebuie remarcat faptul că identitatea și au un loc pentru toate unghiurile la care membrii acestor funcții trigonometrice sunt semnificative. Prin urmare, formula este valabilă pentru oricare altul decât (în caz contrar numitorul este zero și diviziunea cu zero, nu ne-a determinat), iar formula - pentru toate celelalte decât în ​​cazul în care z - orice număr întreg.

Legătura dintre tangenta și cotangentă

Chiar și identități trigonometrice mai evidente decât cele două anterioare, este identitatea care leagă tangenta și cotangentă unghiului de vedere. Este clar că deține pentru orice unghi, altul decât, în caz contrar, fie tangenta sau cotangentă nu este definit.

Dovada formulei este foarte simplu. Prin definiție, și, în cazul în care. A fost posibil să se efectueze dovada și un pic diferit. Așa ca, atunci.

Deci, tangentă și cotangentă unghiului la care face sens, există un număr de reciprocitate.

Tangenta și cosinus, sinus și cotangentă

În cele din urmă, am ajuns la ultimele două identitățile trigonometrice de bază. Ei conecta tangenta și cosinusul și sinus și cotangentă unghiului.

Iată formularea lor: suma pătratului tangenta unghiului și numărul de unități egal cu inversul pătratului cosinusul unghiului, iar suma pătratului unității și cotangentă unghiului este egal cu inversul pătratului sinusul unghiului.

Concluzie Aceste formule pot fi efectuate, pornind de la bază specii identități trigonometrice. Dacă împărțim ambele părți ale acestei ecuații prin (în acest caz, desigur, trebuie să fie diferit de zero), obținem formula. În cazul în care ambele părți sunt împărțite (acest lucru trebuie să fie diferită de zero), ajungem la identitatea.

Astfel, identitatea deține pentru orice distincți de identitate și - în orice alta decât.