Identitatea trigonometrice pitagoreice

Prin corolar 2, tangentă și cosinusul același unghi sunt legate de:

Să ne exprimăm cosinusul ea:

Substituind în această ecuație valoarea setată, obținem

Prin prima identitate trigonometrice principal corolar

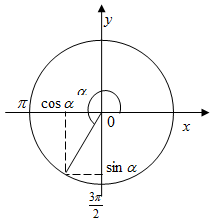
Pentru a determina semnele sinus și cosinus utilizare condiții suplimentare. Deoarece, prin urmare, unghiul se află în al treilea cvadrant (Fig. 4), există cosinus negativ și sine. Apoi, în cele din urmă, obținem

Putem găsi imediat tangenta:

Prin corolar 2 identități trigonometrice de bază, cotangentă și sine sunt legate de:

Ne exprimăm din ea sine:

Substituind în această ecuație, valoarea setată, obținem

Pe primele principale identitățile trigonometrice corolar,

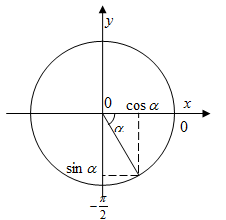
Pentru a determina semnele sinus și cosinus utilizare condiții suplimentare. Unghiul se află în intervalul de aceea, ea face parte din al patrulea trimestru (fig. 5), există o cosinus pozitivă și sinus este negativ. În cele din urmă, obținem