Funcția de distribuție empirică

Să nx - numărul de observații în care valoarea la marca-X mai mică de x. Atunci când mărimea eșantionului egală cu n, frecvența relativă a X-evaluat eveniment <х равна nx /n .

8. Determinarea Funcția

determinarea pentru fiecare valoare a frecvenței relative a evenimentului x X <х, называется эмпирической функцией распреде-ления, или функцией распределения выборки.

Spre deosebire empirică funcția de distribuție F * (x) Funcția de distribuție a probei F (x) generală sovokupnos minute se numește funcția de distribuție teoretică. Time-distincție între cele două este faptul că funcția F (x) a definit-doresc să instituie probabilitatea evenimentului X <х, a F*(x) — относительную частоту этого события. Из теоретических результатов общей теории вероятностей (закон больших чисел) следует, что при больших п вероятность отличия этих функций друг от друга близка к единице:

Este ușor de observat că F * (x) are toate proprietatile F (x), care rezultă din definiția (18,49):

1) valorile F * (x) aparțin intervalului [0, 1];

2) F * (x) este o funcție descrescătoare;

Aceeași funcție F * (x) este utilizat pentru a evalua funcția de distribuție teoretică F (x) din totalul populației.

Exemplul 3. Construct Funcția de distribuție empirică pentru o probă dată:

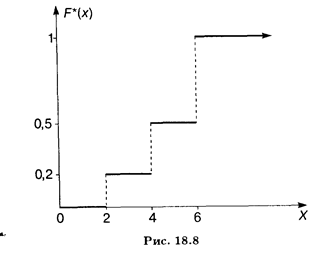
Decizie. Găsiți n mărimea eșantionului = + 15 + 10 = 25 50. Cea mai mică realizare este egal cu 2, deci F * (x) = 0 pentru x ≤ 2. Valoarea X <4 (или x1 = 2) наблюдалось 10 раз, значит, F*(x) = 10/50 = 0,2 при 2 <х <4. Значения X <6 (а именно x1 = 2 и x2 = 4) наблюдались 10 + 15 = 25 раз, значит, при 4 <х <6 функция F*(x) = 25/50 = 0,5. Поскольку x = 6 — максимальная варианта, то F*(x) = 1 при х> 6. Scrieți o formulă pentru funcția empirică necesară:

Graficul acestei funcții este prezentată în Fig. 18.8.

Poligon și histograma

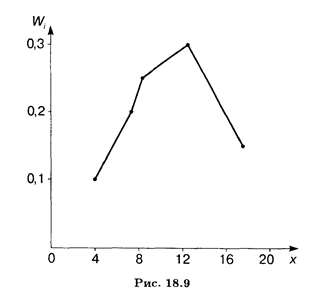
Fiecare pereche de valori (xi. Ni) de distribuție a eșantionului poate fi interpretată ca un punct pe planul de coordonate. Mai precis, dar, de asemenea, poate fi considerată o pereche de valori (x i. Wl) mente privind distribuția eșantionului. segmente de linie poligonale care conectează punctele (xi. Ni), numite frecvențe poligon. Lo manaya punctul de conectare pe planul de coordonate (xi. Wi), frecvențele relative numite poligon. Fig. 18,9 arată distribuția frecvenței relative poligon dată în Exemplul 2.

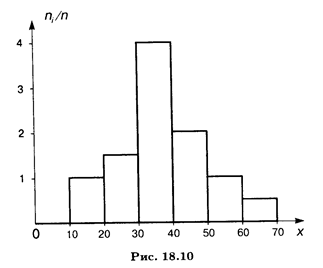
Pentru cazul continuu X caracteristică convenabil pentru a diviza in-interval (xmin. Xmax) din valorile observate pe mai multe subintervale de lungime h fiecare, și de a găsi pentru fiecare din aceste intervale suma frecvențelor Nj. a lovit-l. Etapele chataya formă constând din dreptunghiuri cu baze lungime și înălțime h nj / h (densitatea de frecvență) se numește frecvențele histogramei. Geometrică sensul histogramei: este ușor de văzut că zona sa este egală cu suma tuturor frecvenței sau volumul eșantionului. Fig. 18,10 prezintă o histogramă Ob-EMA n = 100.

In mod similar a determinat și o histogramă a frecvențelor relative în dreptunghiuri înălțime-ing caz care constituie o formă în trepte sheniyami cantități de frecvențe relative otno-determinate în intervalul (xmin + (j - 1). H xmin + jh) Lungimea interval h, adică E-valoare Wj / h. Este ușor de observat că zona histograma frecvențelor relative egal cu unitatea (suma frecvenței relative de eșantionare).