Funcția de distribuție empirică - studopediya

Determinarea funcției de distribuție 25.2.Empiricheskoy funcției apel (funcția de eșantionare), determinarea pentru fiecare valoare a frecvenței relative a evenimentului, și anume,

în cazul în care - numărul mai mic; - mărimea eșantionului.

Din teorema lui Bernoulli rezultă că, pentru o dimensiune suficient de mare eșantion și caracteristici diferă puțin unul față de celălalt. Spre deosebire de funcția de distribuție empirică teoretic este că funcția de distribuție teoretică determină probabilitatea evenimentului, iar funcția empirică determină frecvența relativă a aceluiași eveniment.

Funcția de distribuție empirică posedă toate proprietățile funcției de distribuție cumulativă:

1) valori ale funcției de distribuție empirică aparțin segmentului;

2) - o funcție non-descreștere;

3) în cazul în care - cel mai mic exemplu de realizare, atunci când; în cazul în care - varianta cea mai mare, atunci când.

Exemplul 25.1. Pentru a construi o funcție de distribuție empirică în acest eșantion:

Decizie. Găsim mărimea eșantionului: 12 + 18 + 30 = 60.

2. Cea mai mică variantă este, prin urmare, la.

Valoarea, și anume, au fost de 12 ori, prin urmare, cu.

Valoarea, și anume, și a observat 12 + 18 = 30 de ori, prin urmare, atunci când.

Deoarece - varianta cea mai mare, atunci când.

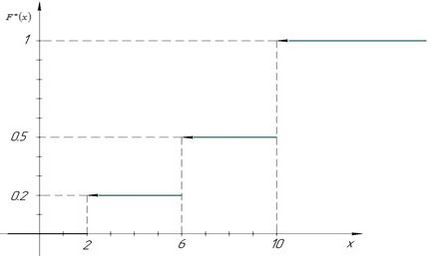
Căutând funcția empirică

Graficul acestei funcții este următoarea: