Formula momentului de inerție, j

Momentul de inerție

Momentul de inerție față de axa în jurul căreia rotația - o măsură de inerție a corpului, prin rotație.

Momentul de inerție este un scalar (în cazul general al tensorului) mărimea fizică, care sunt piese ca suma maselor de la punctul () (care ar trebui să fie efectuate de organism într-o partiție) la distanțele la pătrat () dintre ei cu axa de rotație:

În cazul în care organismul este considerat continuu, însumarea în expresia (1) se înlocuiește cu integrarea, masa corporală a elementelor este desemnat ca:

în care r - o funcție a poziției unui punct material în spațiu; - densitate; este volumul elementului corp. În cazul în care organismul este omogen:

Momentul de inerție al punctului material

rol de masă în mișcarea punctului de material efectuează momentul circumferențială de inerție (J), care este egal cu:

r- în care distanța de la punctul de material pe axa de pivotare. Pentru un punct material care se deplasează de-a lungul circumferinței, momentul de inerție este constantă.

Momentul de inerție este o cantitate de aditiv. Acest lucru înseamnă că, în cazul în care sistemul nu este unul, ci mai multe puncte de material, momentul de inerție (J) este suma momentelor de inerție () puncte distincte:

Exemple de momentele de inerție ale unor organisme

Momentul de inerție al unei tije subțiri de rotație în jurul unei axe care trece printr-un capăt și perpendicular pe tija, este egală cu:

Momentul de inerție al unui con circular drept, masa înălțimea h și raza r se rotește în jurul axei sale:

Momentul de inerție al unui paralelipiped solid uniform, c parametrii geometrici și masa m se rotește în jurul său diagonală cea mai lungă, se calculează cu formula:

Momentul de inerție al unei plăci dreptunghiulare subțiri de masă m, lățimea w și lungimea d, se rotește în jurul unei axe care trece prin punctul de intersecție al diagonalelor dreptunghiului perpendicular pe planul plăcii:

unde m - masa mingii; R - raza sferei. Mingea se rotește în jurul unei axe care trece prin centrul său.

Exemple de formule de calcul momentele de inerție ale celorlalte organisme sunt disponibile în „moment de inerție“. În această secțiune puteți face cunoștință cu teorema lui Steiner.

Exemple de rezolvare a problemelor privind „Momentul de inerție“

Două șirag de mărgele mici de masă m, fiecare conectat la o tijă subțire fără greutate a cărei lungime este egală Care este momentul de inerție al sistemului în jurul unei axe care se extinde perpendicular pe axul prin centrul sictemy în masă?

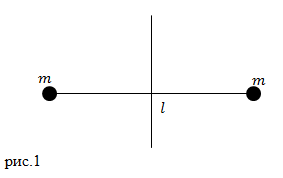
Pentru a rezolva problema vom folosi formula pentru momentul de inerție al unui punct material:

în cazul în care distanța de la punctul la axa de rotație este egală. Prin urmare, formula (1.1) este transformată în:

Deoarece masele de prima și a doua puncte materiale sunt distanță egală de fiecare dintre ele pe axa de rotație, atunci:

Momentul de inerție este valoarea aditiv înseamnă că momentul de inerție al celor două puncte și pentru a găsi ca suma:

Ce moment de inerție, care este prezentat în figura 2 și este format din două tije subțiri, cu mase m. Unghiul dintre tijele drepte. Lungimile barelor sunt egale l. Axa de rotație este paralelă cu una dintre tijele (Figura 2).

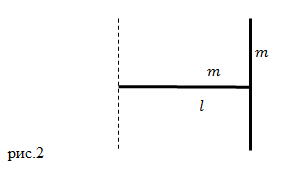
Momentul de inerție poate fi găsit ca suma momentelor de inerție al fiecărei tije în raport cu axa de rotație:

Momentul de inerție () la bara orizontală este:

Găsim momentul de inerție al tijei paralel cu axa de rotație. Pentru a face acest lucru, selectați această tijă de masă punct material. Pentru momentul său de inerție în raport cu axa menționată în figura 2 este:

unde l - distanța orizontală de la masa la axa de rotație, atunci când tija se deplasează nu este schimbat.

Găsim momentul de inerție al întregii tijei () pentru această sumă similară (2.3) momentele de bază ale inerție, precum și o tijă continuă, în locul sumei vom lua integrala:

Derulați până la momentul dorit de inerție al unui sistem de tije: