Distribuția normală (distribuție Gauss)

Aparatul statisticii matematice este destul de bine dezvoltat în raport cu starea, atunci când distribuția variabilei aleatoare respectă o distribuție normală (legea lui Gauss).

Studii în inginerie mecanică a constatat că cele mai multe dintre caracteristicile proceselor tehnologice este obiectul prezentei legi.

Distribuția normală joacă un rol crucial în toate domeniile de inginerie și tehnologie, și ocupă o poziție specială printre celelalte legi ale distribuției.

Distribuția normală a variabilei aleatoare apare în acele cazuri în care rezultatul testului este o consecință a mai multor factori, printre care nu sunt dominante, iar volumul de observare este suficient de mare. Multe monitorizarea continuă cu creșterea volumului de testare tinde la distribuția normală.

O variabilă aleatoare are o distribuție normală, în cazul în ecuația funcției densitate de probabilitate este:

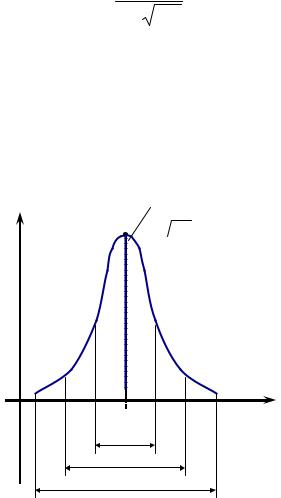
Curba teoretică a dreptului de distribuție normală este în formă de clopot, simetrice în raport cu perpendiculara pe axa x care trece prin punctul de pe axa x cu coordonata Y. Acesta atinge un maxim în acest moment (0 1 σ 2 π) se apropie de zero asimptotic

Așteptarea: M (Y) = Y 0. Dispersia: D (Y) = σ 0 2.

Aria de sub curba mărginită de interval Y 1 ≤Y ≤Y 2. 0 corespunde cu probabilitatea ca rezultatele experimentale vor cădea în fantă. În termen de ± 3σ de la 0 Y 0 este 99,73% din aria de sub curbă.

Prin urmare, în practică, pentru distribuția normală este folosit „regula de trei sigma“. Pentru legea de distribuție normală bazată pe „regula de trei sigma“ câmpul de împrăștiere p a variabilei aleatoare este:

p = (Y o + 3 σ o) - (Y o - 3 σ o) = 6 σ o.

Datorită faptului că estimarea 0 și x sigma 0 folosind caracteristicile eșantionului S și x, câmpul rătăcit practic se determină prin formula:

unde l - valoare tabel coeficient luate pentru o mărime a eșantionului dat pentru α = 0,95 (în care l, se calculează cu condiția ca numărul de variabile aleatorii care sunt în domeniul parazită practic este 99,73%).

Exemple de distribuția normală sunt:

- distribuția erorii mijloacelor de măsurare;

- măsurarea parametrului caracteristic în același lot de produse;

- eroare de poziționare a CNC mașini-unelte, roboți, etc.