Distanța dintre liniile oblice

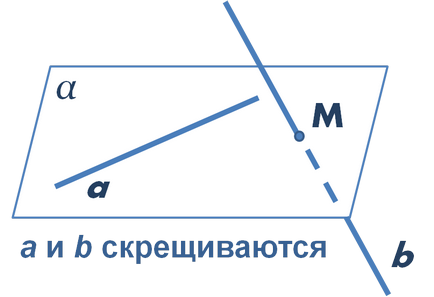
În acest articol un exemplu de rezolvare a problemei C2 USE metoda de a găsi distanța dintre liniile oblice prin metoda de coordonate dezasamblat. Să ne amintim că liniile sunt skreschivayuschi-Misia, în cazul în care nu se află într-un singur plan. În special, în cazul în care o linie se află într-un plan, iar a doua linie dreaptă intersectează acest plan într-un punct care se află pe prima linie dreaptă, aceste linii drepte sunt oblic (vezi. Figura).

Pentru a găsi distanța dintre liniile oblice trebuie să:

1. Prin cea directă a planului oblic, care este paralelă cu celelalte linii oblice.
2. Inferior perpendicular din orice punct de pe planul obținut a doua linie dreaptă. Lungimea perpendiculare va fi distanța dorită între linii.

Să considerăm algoritmul în detaliu pe exemplul de rezolvare a problemei examenului C2 la matematică.

Distanța dintre liniile drepte în spațiul

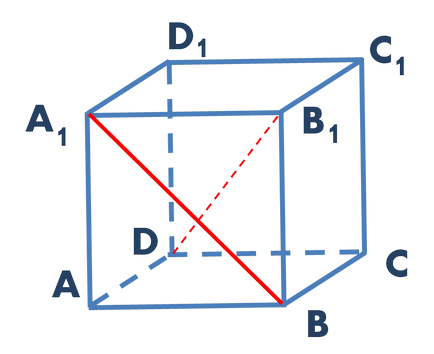
Fig. 1. Planurile de sarcină

Decizie. DB1 în diagonală prin mijlocul cubului (punctul O) trage o linie dreaptă paralelă cu linia A1B. Punctele de intersecție ale drepte coaste linia BC și A1D1 denumite respectiv N și M. Direct MN MNB1 se află într-un plan paralel cu linia și A1b. care, în acest plan nu mint. Aceasta înseamnă că linia este paralelă planul A1B MNB1 pe baza liniei paralele și un plan (fig. 2).

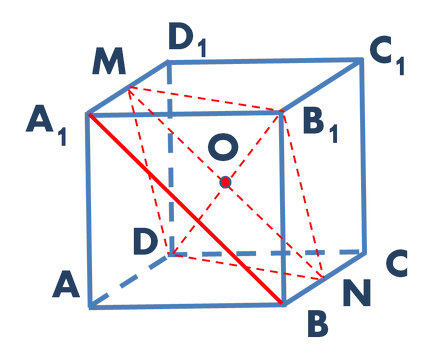
Fig. 2. Distanța necesară între liniile oblice egale cu distanța de la orice punct al liniei selectate pentru planul imaginii

Cautam acum distanta de la orice punct al liniei la planul A1B MNB1. Această distanță va fi, prin definiție, este distanța dorită între liniile oblice.

Pentru a determina această distanță prin utilizarea coordonatelor. Introducem un sistem de coordonate cartezian rectangular, astfel încât originea sa coincide cu punctul B, axa X este orientată de-a lungul marginilor BA. de-a lungul marginii BC - axa Y. axa Z - de-a lungul marginii BB1 (figura 3).

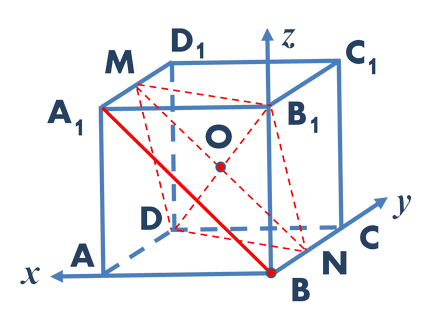
Fig. 3. Sistemul de coordonate cartezian rectangular este ales astfel încât așa cum se arată în figura

MNB1 găsi ecuația planului sistemului de coordonate. Pentru a face acest lucru coordonatele punctelor definesc primul M. N și B1. Rezultat a coordonatelor substitut în ecuația generală a unei linii drepte și se obține următorul sistem de ecuații:

Din a doua ecuație obținem din treimea obținem apoi dintr-o primă se obține Substituind valorile obținute în ecuația generală a unei linii:

Observăm că altfel ar MNB1 avionul trece prin origine. Împărțim ambele părți ale acestei ecuații pe și de a obține:

Distanța de la un punct la un plan definit de formula:

unde - coordonatele punctului B. - coeficienții variabilelor din ecuația planului. Punctul B are coordonatele în cele din urmă se obține: