Dispunerea reciprocă a liniei și de cerc, platforma de conținut

Poziția relativă a liniei și a cercului clarifica cât de multe puncte în comun și pot avea o circumferință dreaptă, în funcție de dispunerea lor reciprocă. În mod evident, în cazul în care o linie trece prin centrul cercului, apoi se intersectează circumferința în cele două capete ale unui diametru, situată. Acest lucru aprox.

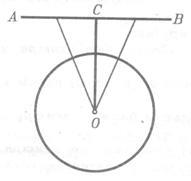
Să linia P nu trece prin centrul O de rază r cercului. Perpendiculara pe linia OH și p notam cu d lungimea perpendiculară T. E, distanța de la centrul cercului la linia (Fig. 1). Investiga dispunerea reciprocă a liniei și a cercului, în funcție de raportul dintre d și r. Trei cazuri sunt posibile.

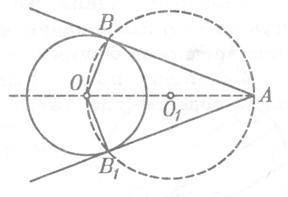
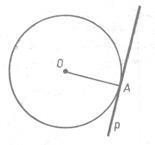
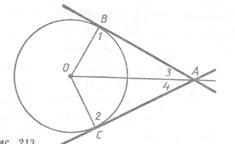
1) d

0B = Prin urmare, punctele A și B Minciuna pe un cerc, și, prin urmare, sunt puncte comune ale liniei p și un cerc dat.

Arătăm că linia p și acest cerc nu au puncte comune. Să presupunem că au un alt punct comun C. Apoi, triunghiul isoscel-median OD SLA. trase la baza UA, aceasta este înălțimea triunghiului, așa ODP. segmente de DO și nu se potrivește

deoarece segmentul D, punctul de mijloc de curent alternativ nu se execută la punctul H - segmentul de mijloc, AB. Am înțeles din punctul O a avut loc două perpendiculare: OH și OD - la linia p, ceea ce este imposibil. Astfel, dacă distanța de la centrul cercului la linia de rază mai mică decât circumferința (d <р),топрямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.

2) d = r. În acest caz, OH = r, r. F. Punctul H este situat pe un cerc, și, prin urmare, este linia punct și arma cercul (Fig. 1b). cerc direct p și nu au alte puncte comune, deoarece pentru fiecare linie M punct p. Spre deosebire de punctul H, OM> OH = r (OM înclinat mai perpendicular OH) și, prin urmare, punctul M nu se află pe cerc. Deci, în cazul în care distanța de la centrul cercului la linia este egală cu raza cercului drepte și au doar un singur punct comun.

3) d> r În acest caz, -OH> r așa. pentru orice punct M 0M linia p OH.> r (fig. 1, a) M De aceea punct nu se află pe cerc. Astfel, .la distanța de la centrul cercului la linia mai mare decât cercul rază, linia dreaptă și cerc sunt disjuncte.

Noi am demonstrat că linia și cercul poate avea unul sau două puncte în comun, și să nu aibă nici un punct comun. O linie dreaptă care are un cerc cu un singur punct comun, numit tangenta la un cerc, iar punctul lor comună se numește punctul de atingere a liniei și un cerc. In figura 2, linia p - tangent la un cerc cu un centru O și A este punctul de tangență.

Demonstrăm o teorema pe proprietatea unei tangenta.

Teorema. Tangenta la cercul perpendicular pe raza realizată la punctul de tangență.

Dovada. Fie p - tangent la un cerc cu centrul O. A - punctul de tangență (a se vedea figura 2 ..). Dovedim. p că tangenta este perpendicular pe raza OA.

Să presupunem că acest lucru nu este cazul. Apoi, OA raza este înclinată spre linia p. Deoarece perpendiculara trase din punctul O la linia dreaptă r, este mai puțin înclinat OA. distanța de la centrul cercului O la linia mai mică decât raza r. Prin urmare, linia p și cercul are două puncte în comun. Dar aceasta contrazice condiția; linia p - tangentă. Astfel, linia p perpendicular pe raza OA. Teorema este demonstrată.

Luați în considerare două tangente la un cerc cu centrul O. care trece prin punctul A și pe circumferință la punctele B și C (fig. 3). Segmentele AB și AC segmente de apel tangentă la punctul A. Acestea au proprietatea care rezultă din teorema:

Segmentele tangente la cercul trase dintr-un singur punct, sunt egale și de a face unghiuri egale cu linia care trece prin acest punct și centrul cercului.

Pentru a dovedi acest lucru, să ne întoarcem la figura 3. Prin teorema de pe proprietatea tangenta unghiurile 1 și 2 sunt drepte, astfel încât triunghiurile ABO și ASO dreptunghiulare. Ele sunt, deoarece acestea au un OA ipotenuză comune și picioare egale de OB și OC. Prin urmare, AB = AC = 3 și 4, după cum este necesar. Demonstrăm acum o teorema, teoreme inverse pe proprietățile tangenta (un semn al tangenta).

Teorema. Dacă linia trece prin raza capătului situată pe cerc și perpendicular pe raza, onayavlyaetsya tangent.

Dovada. Din starea teoremei că raza este perpendiculară trasată de la centrul cercului la linia de date. Prin urmare, distanța de la centrul cercului la linia este egală cu raza, și, prin urmare, linii și cercuri au doar un singur punct comun. Dar acest lucru înseamnă că linia este tangenta la cercul, QED.

Această teoremă are la bază de rezolvare a problemelor pentru a construi o tangentă.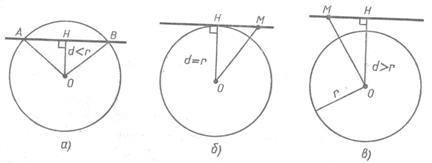

Direct și circumferința pot fi în următoarele trei poziții relative în mod evident, numai:

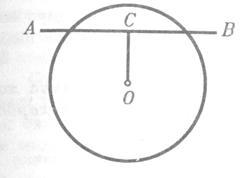
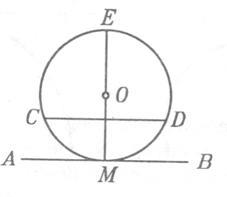
1) Distanță (OS) de la linia centrală (AB) (m. E OS lungime perpendicular, a scăzut de la centru, pe o linie dreaptă) este mai mare decât raza cercului (Fig. 1). Apoi, cu un punct de drept este la distanță de centru este mai mare decât raza, și, prin urmare, se află în afara cercului. Deoarece toate celelalte puncte de pe linia sunt îndepărtate de la aproximativ mai mult decât punctul C (panta distanta perpendicular), toate acestea se află în afara cercului, apoi, în timp ce în linie dreaptă nu are puncte în comun cu cercul.

2) Distanță (OS) a liniei mediane de rază mai mică. În acest caz (Figura 2), punctul C este în interiorul cercului și apoi, în mod evident, linia intersectează cercul.

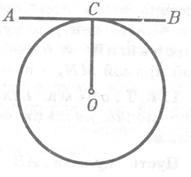
3> Distanță (OS) de la linia centrală egală cu raza. Apoi precis C (fig. 3) și aparține linia dreaptă și un cerc, toate punctele rămase ale liniei, fiind îndepărtat de la O mai mult punctul C. se află în afara cercului. Prin urmare, în acest caz, liniile drepte și cercuri au un singur punct comun, și anume cea care formează baza perpendicularei din centrul pe o linie dreaptă.

O astfel de linie, un cerc care are doar un singur punct comun, numit tangenta la cercul; punct comun se numește punctul de contact.

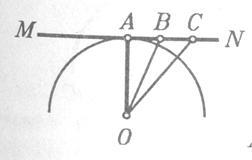
Relativ la tangenta, dovedim următoarele două teoreme (înainte și invers) (Figura 4.):

1) în cazul în care linia (MN) este perpendicular pe raza (OA), la capătul său (A) situată pe un cerc, se kasaetsyaokruzhnosti și de transfer (figura 4) .;

2) în cazul în care o linie tangentă la cercul, raza trase la punctul de contact, perpendicular pe acestea.

1) punctul A ca raza capătului situată pe circumferința cercului aparține; În același timp, ea aparține directe MN, aceasta înseamnă că acest punct este comun în cerc și drepte. Toate celelalte puncte de pe linia MN, ca B, C, și altele, sunt separate de centrul O mai departe decât raza (ca OB segmente, OC. Ambele înclinate OA mai perpendicular), și pentru că acestea se află în afara cercului. Astfel, linia MN este doar un singur punct (A), cu o circumferință totală, și, prin urmare, există o MN linie tangentă.

2) În cazul în care MN este tangent la cercul de la punctul A, toate celelalte puncte ale acestei linii trebuie să se situeze în afara cercului; Prin urmare, segmentele OB, OC. mai mare decât raza OA (punctul O este centrul cercului). Deci, această rază este cea mai mică dintre segmentele care se conectează punctul O la orice punct al liniei MN, și pentru că OA | MN.

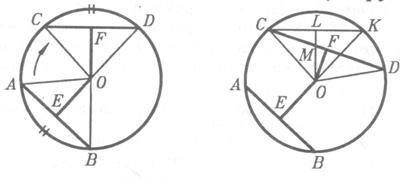
Teorema. În cazul în care tangenta este paralelă cu coardă, apoi punctul de contact care împarte arc subîntins coardă în jumătate.

Lăsați linia AB tangenta la cercul de la punctul M (figura 5.) și paralel cu coarda CD; necesară pentru a dovedi că.

Desen prin punctul de diametru tangență UI. avem :; prin urmare

Relația dintre arce, acorduri și distanța coardă de centru.

Teorema. Într-un cerc sau în cercuri egale:

1) în cazul în care arcul sunt egale, atunci strângerea corzile lor sunt egale și echidistante față de centru;

2) În cazul în care cele două arce, mai puțin de un semicerc, nu sunt egale, cele mai multe dintre ele contractate de mai multe acorduri și acorduri de ambele mari situate mai aproape de centru.

1) Să arc AB este egal cu CD arc (Fig. 1), este necesar pentru a dovedi că coarda AB și CD sunt OE egale, egal și perpendicularele și OF, a redus de la centru la o coardă.

OAJB roti sectorul în jurul centrului O în direcția indicată de săgeată, astfel încât raza OB a coincis cu sistemul de operare. Apoi, arcul BA. Se merge de-a lungul CD-ul cu arc, și din cauza egalității lor alinia arc. Prin urmare, AS coardă aliniată cu CD-ul coardă și DE coincide cu perpendiculara (de la un punct poate fi coborâtă la o singură linie perpendiculară) t. E. AB = CD si OE = OF.

. 2) Fie arc AB (figura 2) este mai mică decât CD-ul cu arc, și, în plus, atât arcul mai puțin decât un semicerc; Este necesar să dovedească faptul că coarda AB mai mică decât CD-ul coardei, și OE perpendicular mai perpendiculara. Amînarea arc CD SC arc egal cu AB, și trage o coardă auxiliară IC. care a fost demonstrat, coarda AB egal și la fel este eliminat din centru. In triunghiuri COD și suc sunt două fețe ale unuia sunt egale cu cele două laturi ale unei alte (ambele raze), iar unghiurile încheiate între aceste părți nu sunt egale; în acest caz, după cum știm, împotriva mai multor unghiuri, adică. e. lCOD, ar trebui să se bazeze pe latura mare, apoi, CD-uri> CK, și pentru că CD-ul> AB.

Pentru a dovedi că OE> OF, OLXCK efectueze și să ia în considerare ceea ce a fost demonstrat, OE = OL; Prin urmare, avem nevoie decât să compar împreună cu OL. Într-un triunghi dreptunghic 0FM (acoperit în Figura accidentul vascular cerebral) peste picior OM ipotenuza; dar OL> OM; apoi, a fortiori, OL> OF. și pentru că OE> A.

Teorema ne-a dovedit a fi pentru un singur tur, rămâne valabil pentru cercuri egale, pentru că aceste cercuri se deosebesc unul de altul numai în poziția.

teoreme Inverse. Așa cum sa discutat în secțiunea anterioară toate cazurile posibile se exclud reciproc în ceea ce privește valorile relative ale celor două arce de aceeași rază, în care concluziile strung se exclud reciproc cu privire la cantitățile relative de acorduri și distanțele lor de centru, propunerile inverse ar trebui să fie luate în considerare în mod corect. și anume:

Într-un cerc sau cercuri e egale:

1) coardele egale echidistante față de centru și egale de strângere a arcului;

2) coardă, la aceeași distanță de centrul sunt egale și egale de strângere a arcului;

3) a două acorduri inegale mari mai aproape de centru și trage un arc mare;

4) din cele două coardele inegal de centru, care este mai aproape de centru, mai mult și trage un arc mare.

Aceste propuneri pot fi ușor dovedit prin contradicție. De exemplu, pentru a dovedi primul dintre ele motivat că în cazul în care datele din coarda arcului legat inegal, în conformitate cu teorema directă nu, ei ar fi egal, ceea ce contrazice ipoteza; înseamnă acorduri egale trebuie să tragă arce egale; dar, în cazul în care arcul este egal, conform teoremei Direct, strângerea coardele lor sunt echidistante de centru.

Teorema. Diametrul este mai mare de acorduri.

Dacă vă conectați cu centrul la sfârșitul oricărui acord care nu trece prin centrul, cum ar fi coarda AB obținem triunghiul AOB, în care una dintre părți are acest acord, iar celelalte două (Figura 3.) - razele, dar în triunghiul, fiecare parte mai mică decât suma celelalte două laturi; prin urmare, coardă AB mai mică decât suma a două raze; întrucât fiecare CD diametru este suma celor două raze. diametru mediu este mai mare decât oricare din coarda care nu trece prin centrul. Cu toate acestea, din moment ce diametrul este, de asemenea, o coardă, se poate spune că diametrul este mai mare de acorduri.

După cum sa menționat deja, segmentele unei tangente la circumferința unui punct au aceeași lungime. Această lungime se numește tangenta distanța de la punctul de la circumferința.

Fără o teoremă tangentă nu eliberează soluția nu este o problemă a cercului înscris, cu alte cuvinte, a tangenta cercului pe laturile poligonului.

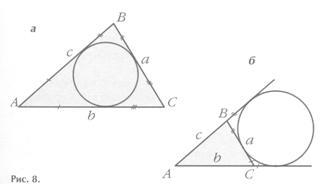
distantele tangențiale în triunghi.

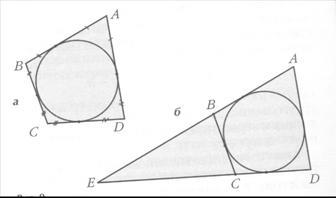
Noi găsim lungimile segmentelor în care latura triunghiului ABC divizat puncte de tangență cu un cerc înscris în ea (fig. 1a), astfel distanța tangențială ta de la un punct A la un cerc. Punerea laturi b și c. și apoi scade cantitatea de partea laterală a unui. Având în vedere egalitatea de tangente trasate dintr-un nod, obținem 2TA. Astfel,

unde p = (a + b + c) / 2 - jumătate de perimetru al triunghiului. Lungimea laturilor segmentelor adiacente nodurile B și C sunt, respectiv, p-b și p-c.

In mod similar, pentru triunghiul tangent cercului este descris (în afara) lateral și (fig. 1b), distanța de la tangent B și C sunt, respectiv, p-c și p-b. și din partea de sus a A - doar p.

Rețineți că aceste formule pot fi utilizate „în sens invers“.

Să presupunem că unghiul BAC este înscris cerc, tangenta distanța de la nodul la circumferința ravnop ilip-a. gdep - jumătate de perimetru al triunghiului ABC. și a = BC. Apoi cercul este tangent la linia BC (respectiv în afara sau în interiorul triunghiului).

De fapt, lasa, de exemplu, distanța tangentă este p-o. Apoi cercurile noastre ating laturile unghiului în aceleași puncte ca cercul înscris al triunghiului ABC. și, prin urmare, coincide cu ea. Prin urmare, este vorba despre Soare directă

patrulater tangențiale. Din teorema egalității de tangențială obținut imediat (Fig. 2a), care

În cazul în care patrulaterul este posibil să se înscrie într-un cerc, atunci suma dintre laturile sale opuse sunt egale:

Rețineți că patrulater tangențial în mod necesar convexe. Opusul este adevărat:

Dacă un patrulater convex și cantitatea de laturile sale opuse este egală, atunci cercul poate fi înscris în ea.

Să ne dovedesc acest lucru pentru o alta decât un paralelogram patrulater. Să oricare două părți opuse ale unui patrulater, de exemplu AB și DC, continuând în același timp să se intersecteze în punctul E (fig. 2b). Înscriem un cerc în triunghiul ADE. Sale tangent distanta te la punctul E este exprimat prin formula

Dar starea valoarea laturile opuse ale unui patrulater sunt egale, și, astfel, AD + BC = AB + CD. sau AD = AB + CD-BC. Substituind această valoare în expresia te. obținem

iar acest lucru - jumătate din perimetrul triunghiului ien. Din condiția sa dovedit mai sus ar trebui să atingă cercul nostru este tangentă la BC.

Două tangent la cercul dintr-un punct în afara acesteia, sunt egale și formează unghiuri egale cu o linie care leagă acest punct spre centru, care rezultă din ecuația unghi triunghiuri AOB și AOV1