Cum să se plieze hârtia și să-l pe Lună

Cunoașterea principiilor de progresie geometrică ne ajută în viața de zi cu zi, de acumularea de dobânzi la depozit, la viteza de învățare de propagare a epidemiilor. De asemenea, progresia geometrică se află în centrul celebrului paradox, o provocare înțelegerea noastră infinit.

Ia o foaie de ziar. De câte ori poți să-l ori în jumătate? În lumea reală, un număr maxim de șapte ori (încercați să-l tine). Dar să ne imaginăm că putem pune această foaie de câte ori ne-o dorim. Deci, dacă ai pus o foaie de hârtie doar de 45 de ori, grosimea straturilor va fi atât de mare încât ar ajunge la luna.

Să vedem de ce.

Să presupunem că o grosime foaie de ziar de 0,001 cm Dacă jumătăți de foi pliate, grosimea este dublată și va fi 0.002 cm și cu fiecare adăugare succesivă de jumătate din grosimea va menyatsyav conformitate cu secvența: .. 0,001grame cm, 0,002 cm, 0,004 cm, 0,008 cm, 0,016 cm , 0,032 cm ...

Plierea foaia în jumătate de zece ori. vom obține o grosime de 1 cm ziar * 10 * 2 -3 10 sau 1.024, a se vedea, că este un pic mai mult de un centimetru. Este necesar să se stabilească de 17 ori - nu este o problemă - a obține un 1 cm x 10 -3 17 * 2 = 131 cm, înălțimea hobbit medie.

Glumele sunt peste, acum serios.

Fold de treizeci de ori - aproape zece kilometri (1 cm * 10 -3 * 2 30). La aceasta altitudine avioanele zboară! Patruzeci de ori - aproape 11 000 km (1cm x 10 -3 40 2 *). Houston are un decalaj! La această altitudine pe orbită sateliți în orbită: de 43 de ori: 87 961 km, de 44 de ori: 175,921 km, de 45 de ori: 351 844 km. Stop! Am ajuns pe Lună! Dacă adăugați o foaie de hârtie încă o dată, atunci ne putem întoarce pe Pământ!

Acest tip se numește creștere exponențială (exponent - exponent). Lui natura „explozivă“ este în contrast cu o linie de „lent“, și o creștere a puterii.

Numerele de secvență obținute prin exemplul unui ziar, formează o progresie geometrică.

progresie geometrică - numerică secvență b 1. b2. b3. în care fiecare numere succesive începând cu a doua este formată din cel precedent prin înmulțirea cu un anumit număr q (progresie numitor). În acest caz, b1 ≠ 0 și q ≠ 0, altfel obține doar secvența de zerouri.

unde n - număr întreg.

Vă rugăm să rețineți, să știe totul despre exponențial, este nevoie doar trei parametri: valoarea primului element de B1. q progresie, iar numărul de membri n. În exemplul de grosimea inițială a hârtiei foaie a servit ca prim element, precum și faptul că, prin adăugarea a doua jumătate ziar foaie grosimea sa este dublată, oferindu-ne q value = 2. Dat fiind faptul că orice element progresie poate fi reprezentat ca o = b1 * q bn ( n-1):

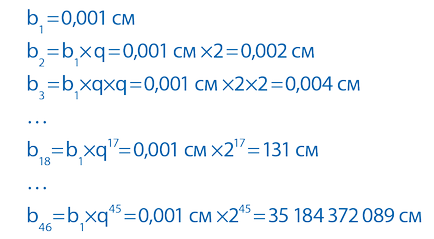
Ca și în progresia aritmetică, este uneori necesar să se calculeze suma tuturor elementelor de progresie. Hai să facem un mic truc. Scriem ecuația după cum urmează, și apoi scade a doua ecuație din prima:

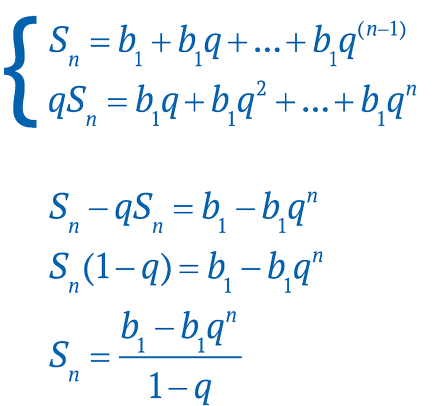
Astfel, obținem formula pentru calcularea sumei unui număr finit de elemente geometrice.

progresie geometrică este baza celebrului paradox, o provocare înțelegerea noastră infinit.

Și dacă elementele în evoluția unui număr infinit? Putem apoi calcula suma acestei progresii? Comportamentul exponențial și se determină cantitatea de q progresie. Și pentru aproape toate valorile q nimic neobișnuit se întâmplă, suma unui număr infinit de elemente geometrice nu duce la ceva finit. Aceasta este, varianța, în cazul în care limbajul matematicii.

Cu toate acestea, în cazul în care progresie geometrică are un număr infinit de elemente și numitorul său este mai mic decât unitatea (q<1 ) представляет особый интерес.

Intuiția ne spune că suma unui număr infinit de elemente pozitive ar trebui să fie, de asemenea, cel puțin, să fie infinit. Este adevărat? Pe această problemă a reflectat drevnegrecheskiyfilosof Zenon Eleysky, în viitor, aceste gânduri a devenit baza pentru așa-numitul paradox dihotomie paradox sau împărțirea în două.

După o zi productivă de reflecție, Zeno a decis să meargă în parc, situat în apropierea casei sale. Să presupunem că distanța până la parc un kilometru, iar Zeno este o viteză de 1 km / h. Cât timp durează o plimbare?

Iată argumentele lui Zeno. Pentru a ajunge la parc, mai întâi trebuie să mergi la jumătatea drumului - ½ km, nu? Este nevoie de o jumătate de oră. De îndată ce a ajuns la mijlocul căii, va trebui să treacă prin jumătate distanța rămasă - ¼ kilometri. Și acest lucru la rândul său, va dura ore ¼. În continuare, se va face de această dată și din nou. Și poate continua așa pentru totdeauna.

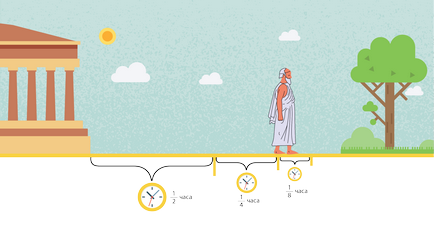
Deci, cât timp Zeno ar merge în parc? Pentru a răspunde la această întrebare, trebuie să adăugați la toate perioadele de timp care au fost cheltuite pe fiecare parte a călătoriei sale. Cu toate acestea, problema este că un astfel de număr infinit de piese!

Vă rugăm să rețineți că următorul termen al secvenței crește cantitatea de:

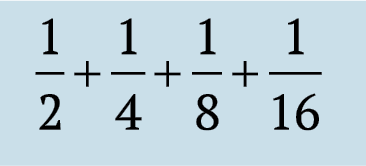
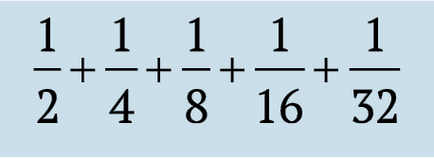
care, la rândul său, este mai mică

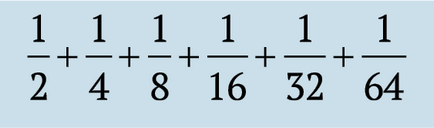
și așa mai departe. Aceasta este valoarea noastră cu fiecare element succesiv este crescut, iar numărul de membri devine infinit de mare, la fel ca în cazul nostru, suma va continua să crească pe termen nelimitat. Prin urmare, o plimbare în parc are o cantitate infinita de timp, cu alte cuvinte, nu ajunge niciodata in parc!

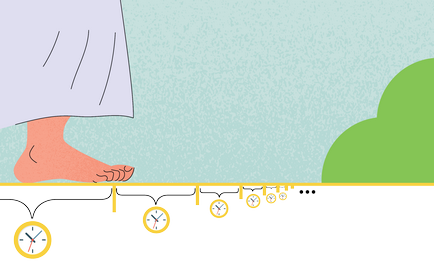
Asta e paradoxul. Pe de o parte, avem de-a face cu o justificare clară pentru Zeno, care susține că orice mișcare este imposibilă, dar pe de altă parte - putem sta în picioare și merge la frigider. Primul gând care apare - absurd!

Dar mintea raționamentul lui Zenon au ocupat matematicieni și filosofi de mii de ani, care a aprofundat înțelegerea infinit și continuitate.

În cazul în care este eroarea în logica Zeno? Ca parte a unui model matematic pentru a calcula mișcarea plimbare este ușor. Într-adevăr, timpul de călătorie - este distanța împărțită la viteza, prin urmare, timpul estimat merge - o oră.

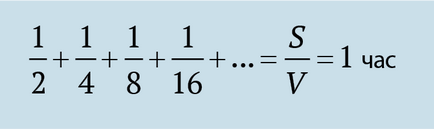
După cum sa dovedit mai târziu, matematică, există momente când este posibil să se rezuma un număr infinit de elemente, și pentru a obține răspunsul final. Aceasta este, după cum spune matematicieni, secvența converge. În cazul nostru, o cantitate infinită de sloturi de timp este egal cu (converge) la o oră.

Așa cum am văzut, secvența infinită obținută de Zeno, este o progresie geometrică. Iar suma acestei progresii este convergentă. Observați numitorul comun al progresiei? Este egal cu ½. Se pare că, atunci când q> -1 q<1 сумма бесконечной геометрической прогрессии сходится. Давайте вспомним формулу для конечной прогрессии и переделаем ее для бесконечного случая.

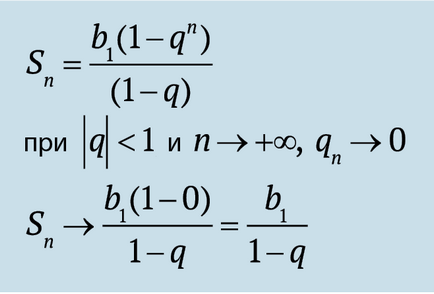
Rezumând, vreau să atrag încă o dată atenția asupra faptului, ca alegerea q progresie determină comportamentul o progresie geometrică. De la o creștere exponențială a degradare exponențială. De la călătorie la luna de pe o bucată de hârtie și la o astfel de valoare mica încât suma lor, chiar și infinit, nu contează.