Cum să înmulțiți cu numărul de rădăcină

Uită-te la rădăcina. Dacă numărul. înregistrată sub rădăcină, este un sistem complet de numere diferite pătrate (1, 4, 9, 16, 25, 36, 49, 64, 81, 100.) extract de rădăcină. Asta EEST obține un număr întreg. pătrat care este un număr. înregistrată sub rădăcină. Înmulțim cu al doilea factor. Notați răspunsul.

În cazul în care rădăcina pătrată nu este eliminat, acesta este, de obicei răspunsul poate fi înregistrat prin simpla îndepărtare a semnului de multiplicare. Se pare numărul. constând dintr-un întreg și o rădăcină din apropiere. Acest lucru ar însemna că rădăcina este luată este un număr întreg de ori. Integer este de obicei scris pe partea stângă a rădăcinii.

Dacă doriți să aduceți toate numerele de la rădăcină. Urmați pașii de mai jos. Ridicați partea întreagă a pătrat. Domnozhte numărul. stând sub rădăcină. Se înregistrează numărul radicand. Acesta va fi răspunsul.

Una dintre cele patru elementare de matematică (multiplicare) a creat o alta, ceva mai complicată - putere. Aceasta, la rândul său, adaugă o complexitate suplimentară la predarea matematicii, dând naștere să se inverseze operațiune - extracția rădăcinilor. Pentru oricare dintre aceste operații pot fi aplicate toate celelalte operații matematice, care îi zăpăcește în continuare studiul subiectului. Pentru ca toate acestea să reglementeze într-un fel, există seturi de reguli, una dintre care reglementează procedura de multiplicare a rădăcinilor.

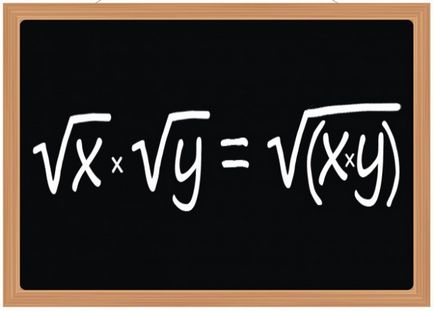
Utilizați pentru a multiplica regula rădăcină pătrată - rezultatul acestei operațiuni ar trebui să fie rădăcina pătrată. expresie radicală, care este produsul radicands rădăcinoase factori. Acest lucru se aplică multiplicarea de două, trei sau orice alt număr de rădăcini pătrate. Cu toate acestea, se aplică nu numai la rădăcinile pătrate, dar, de asemenea, la cub sau orice alt indicator al gradului, în cazul în care rata este aceeași pentru toți cei implicați în chirurgia radicală.

În cazul în care mărcile multiplicate cu valorile numerice ale rădăcinilor sunt apoi înmulțiți-le împreună și a pus valoarea rezultată sub semnul rădăcină. De exemplu, când multiplicată √3,14 pe √7,62 această acțiune poate fi scrisă ca: √3,14 * √7,62 = √ (3,14 * 7,62) = √23,9268.

În cazul în care radicands conțin variabile, primul a scrie produsul lor sub același semn radical, și apoi încercați să simplifice expresia radicală rezultată. De exemplu, în cazul în care este necesar să se multiplice √ (x + 7) √ (x-14), atunci operația poate fi scrisă ca: √ (x + 7) * √ (x-14) = √ ((x + 7) * (x- 14)) = √ (x²-14 * x + 7 * x-7 * 14) = √ (x²-7 * x-98).

Dacă este necesar, se multiplica mai mult de două rădăcini pătrate acționează în același mod - adună sub un semn radicands radicale toate rădăcinile multiplicate ca un multiplicator de o expresie complexă și apoi simplifica. De exemplu, când înmulțirea cu rădăcina pătrată a numerelor 3.14, 7,62, 5,56 și funcționare poate fi scrisă ca: √3,14 * √7,62 * √5,56 = √ (3,14 * 7,62 * 5 , 56) = √133,033008. O multiplicare a rădăcinilor pătrate derivate din expresiile cu variabilele x + 7, x-14 și 2 * x + 1 - ca: √ (x + 7) * √ (x-14) * √ (2 * x + 1) = √ ((x + 7) * (x-14) * (2 * x + 1)) = √ ((x²-14 * x + 7 * x-7 * 14) * (2 * x + 1)) = √ ((x²-7 * x-98) * (2 * x + 1)) = √ (2 * x * x²-2 * x * 7 * x-2 * x * 98 +-x² 7 * x-98) = √ (2 * Xg-14 * x²-196 * x + x²-7 * x-98) = √ (2 * Xg-13 * x²-205 * x-98).

• regula rădăcină pătrată

Construcția puterii - este o formă redusă a operațiunilor de scriere de multiplicare repetate, în care toți factorii sunt egale cu numărul inițial. O operație de extracție root este invers - definiția factorului care trebuie să fie angajat în multiplicarea operațiuni repetate, astfel încât rezultatul său a fost radicand. Ca o indicație a gradului și rata punctului rădăcină la același lucru - cum ar trebui să fie mai mulți factori într-o astfel de operațiune de multiplicare.

Dacă un număr sau o expresie pe care doriți să se aplice în același timp și exploatarea de a extrage o rădăcină, și ridicând-o la puterea, reduce cele două acțiuni într-o singură - în exponentiere cu exponent fracționată. Numărătorul ar trebui să fie exponent, iar numitorul - rădăcină. De exemplu, dacă doriți să pătrat rădăcina cub. atunci aceste două operații vor fi echivalente cu una dintr-un număr ridicat la puterea de ⅔.

În cazul în care condițiile care urmează să fie ridicată în kvadratkoren cu un exponent egal cu doi, nu este sarcina de calcul, și testa cunoștințele. Profitați de metoda de primul pas, și veți obține fracția 2/2, adică, 1. Aceasta înseamnă că rezultatul construcției în rădăcină kvadratkvadrat picior de orice număr este numărul în sine.

Dacă este necesar, să construiască în kvadratkoren cu un exponent, chiar, există întotdeauna posibilitatea de a simplifica funcționarea. Deoarece cei doi (numărătorul exponentul fracționată), precum și orice număr par (numitor) este un divizor comun, după simplificarea fracțiilor în numărătorul va rămâne o unitate, ceea ce înseamnă că pentru a construi puterea de calcul nu este necesară, este suficient să se ia o rădăcină cu jumătate de exponent . De exemplu, cvadratura rădăcina a șasea putere a opt poate fi redus la extragerea rădăcinii cub de ea, deoarece 2/6 = 1/3.

Pentru a calcula rezultatul în toate exponenții din rădăcină, utilizarea, cum ar fi un calculator, built-in motorul de cautare Google. Aceasta este, probabil, cel mai simplu mod de a decontare în cazul în care există acces la Internet de pe computer. substitut general acceptate pentru ridicarea semnului în funcțiune este un astfel de grad este o „acoperire“: ^. Folositi-l atunci când introduceți o interogare de căutare în Google. De exemplu, pentru a construi un al cincilea grad de numărul kvadratkoren 750 specificați interogarea de 750 ^ (2/5). După introducerea motorului de căutare, chiar și fără a apăsa butonul de trimitere de pe server-ul va afișa rezultatul de calcul până la șapte zecimale: 750 ^ (2/5) = 14.1261725.

• cub rădăcină pătrată