Cum de a rezolva polinoame 1

În matematică, un polinom (sau polinomială) - este suma sau diferența dintre monoamele. Monoamele includ variabile și constante, de exemplu monoamele sunt 4, -10x și 3x 3. Polinomul constă în oricare dintr-un număr finit de monoamele care nu conțin exponenților negativi (x -3), variabilele din numitorul (1 / x) și variabila marcate rădăcină pătrată. Pentru a rezolva un polinom, aveți nevoie pentru a afla pentru ce valori „x“ polinom este zero.

pași Editare

Metoda 1 de la 5:
Înregistrare Editare polinomul

Aranjați termenii polinomiale în ordinea descrescătoare exponenți. Rescrie polinomul, astfel încât membrul cu cel mai mare exponent a fost plasat mai întâi, iar membrul cu cel mai mic grad - ultima. De exemplu, polinomul -1 + 3x 2 - x 5 rescriere ca: - x 5 + 3x 2 - 1.

• Amintiți-vă că termenul negativ este întotdeauna negativ, chiar dacă înregistrarea primei sale. Uită-te la exemplul anterior; membru - x 5 a fost negativ (deoarece scade), asa ca a fost negativ atunci când ați înregistrat primul său membru.

Simplificarea polinomul. Uneori, fiecare termen al polinomului conține un factor care poate fi scos din paranteze și, astfel, a simplifica polinomul. De exemplu, în polinomul 2x 2 + 4x - 12, fiecare membru este divizibil cu 2, adică 2 poate fi scos din paranteze: 2 * (x 2 + 2x - 6), iar valoarea polinomului inițială nu se va schimba. Nu uitați că această metodă este aplicabilă numai atunci când fiecare membru are un factor comun.

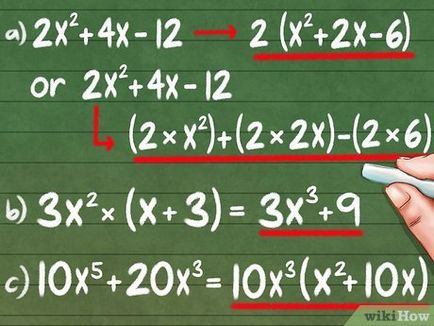
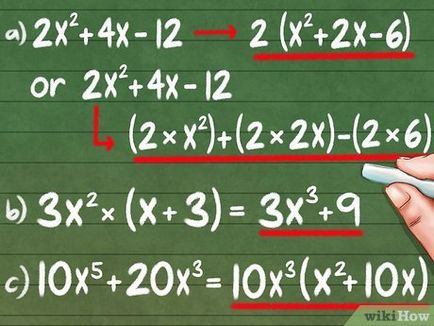
• Pentru a verifica calcul, se multiplica fiecare termen, la rândul său 2. În cazul în care polinomul inițial: 2x 2 + 4x - 12 = (2 * x 2) + (2 * 2x) - (2 * 6)
• Această metodă se aplică, de asemenea variabile, de exemplu: 3x 2 * (x + 3) = 3x 3 + 9x 2.
• Scoateți întotdeauna parantezele de cel mai mare multiplicator. Polinomul 5 10x + 20x 3 paranteze nu numai pot face 2, dar 10x 3. [1]

Determinați dacă puteți rezolva polinom. Nu uitați că polinomul include orice număr finit de monoamele care nu conțin exponenților negativi (x -3), variabilele din numitorul (1 / x) și variabila sub semnul rădăcină pătrată. În cazul în care nu este îndeplinită cel puțin una dintre aceste condiții, atunci ecuația este rezolvată prin metode care nu sunt abordate în acest articol.

• Rețineți că polinoame, al cărui exponent este 4 (x 4) și de mai sus, este foarte dificil de rezolvat, dar este posibil să se utilizeze un calculator grafic.
• Dacă aranja un polinom în ordinea descrescătoare exponenți, acesta va fi înregistrat într-un format standardizat.

Amintiți-vă principalii termeni matematici. Este dificil de rezolvat polinoame, dacă nu cunosc terminologia. Notă următorii termeni:

• Monom (sau membru) - o expresie matematică care implică constante sau variabile și constante și variabile. De exemplu, 5, x, 3t, 15Y 3.
• Polinomială (sau polinomială) - este suma sau diferența dintre monoamele.
• Multiplicatorul - un număr care, atunci când înmulțit cu un alt număr dă al treilea. De exemplu, multiplicatoare 10 sunt numerele 2, 5, 1, 10, deoarece fiecare dintre numerele fiind înmulțit cu un alt număr, da 10. Multiplicatorii poate fi variabilă, de exemplu, 10x multipli monomiale sunt 2, 5, 1, 10 și x.
• Gradul - este cel mai mare exponent al variabilei, care este un polinom. De exemplu, polinomul x 5 + 3x + 55 este un al cincilea polinom de gradul.
• Trinomial - un polinom care constă din trei monoamele, de exemplu, 2x 2 + x + 12.
• Binom (sau fasole) - este un polinom, care constă din două monoamele, de exemplu, x + 9. Rețineți că unele polinoame poate fi descompus în două sau mai multe binomi factori.

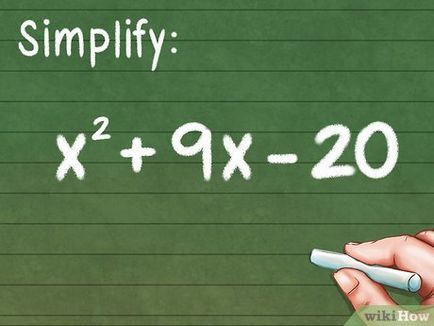
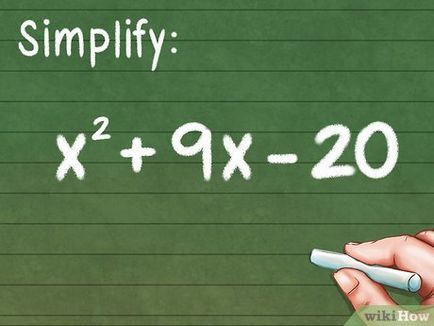
Rezolva polinomială, care este dat ca un trinom. Acest articol discută doar polinomul pătratice (o măsură a gradului este mai mică de 2, de exemplu, x 2. 3x 2, și așa mai departe), deoarece astfel de trinom sunt cele mai comune și ușor de rezolvat. Trinomial trebuie să fie descompus în produs de polinoame de gradul I. Să considerăm un exemplu: x 2 + 9x - 20.

Amintiți-vă că trinomul pot fi luate în considerare în polinoame. Pentru a rezolva trinom, trebuie să-l simplifica și de a face acest lucru pune trinomul pe un produs de polinoame, a cărui exponent nu este mai mare de 1 (de exemplu, x, 5x, și așa mai departe). Amintiți-vă înmulțirea comanda polinoame: primul membru, primul și al doilea element, primul și al doilea, al doilea membri. De exemplu, se înmulțește binomi (x + 3) și (x + 2):

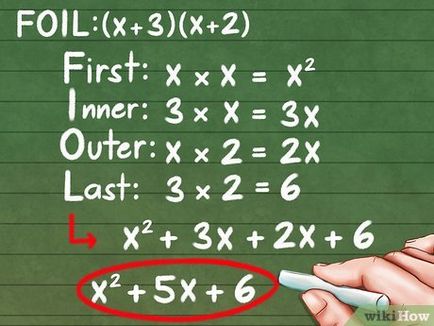
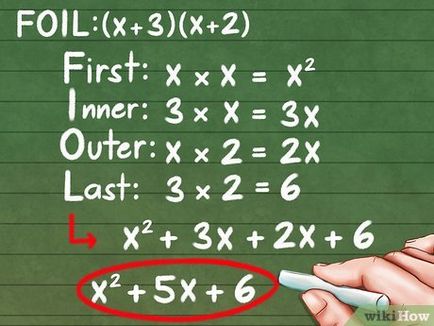
• (X + 3) (x + 2)
• Primii membri. Primii membri sunt „x“.
  • x * x = x 2
• Primul și al doilea termen. Primul element este „X“, iar al doilea 2.
  • x * 2 = 2x
• În al doilea rând și primii membri. 3 este un al doilea membru, iar primul „x“.
  • 3 * x = 3x
• Al doilea termeni. În al doilea rând sunt termeni 3 și 2.
  • 2 * 3 = 6
• Am ori rezultatele pentru a obține un polinom: x 2 + 3x + 2x + 6.
• Fold (sau scade) acești membri pentru a simplifica polinomiale (termeni similari - un membru care cuprinde o variabilă de unul și același exponent): x 2 + 5x + 6

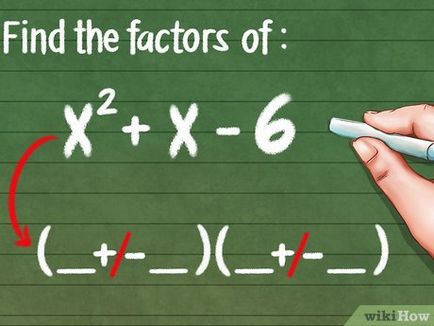
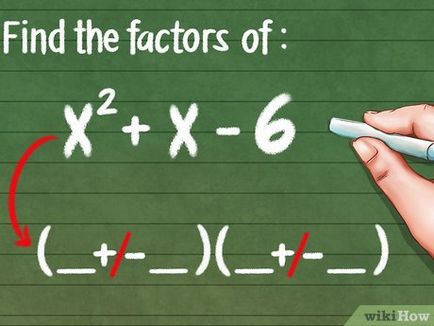
Lay factoring trinom. Majoritatea trinom poate fi descompus în doi factori, dintre care fiecare este un binom de primul grad. Această metodă include o metodă de încercare și eroare. Vă rugăm să rețineți următoarele:

• Primul termen al trinomul (x 2) este rezultatul înmulțirii primii termeni ai fiecărui binom.
• Al doilea termen al trinomul (x) este suma rezultatelor multiplicării primul și al doilea și al doilea și primii membri ai fiecărui binom.
• Al treilea membru al trinomul (6) este rezultatul înmulțirii al doilea termenii fiecărui binom.
• În cazul în care al treilea membru trinomial negativ, al doilea membru al uneia dintre binomi fi negativ.
• expansiune record trinomial produsului de binomi sub forma x 2 + x - 6 = (+/- __ __) (__ + / -__), adică, pentru a găsi monoamele și să le înlocuiască în loc de spații.

Găsiți primele monoamele (pentru fiecare pereche de paranteze). Luați în considerare acest exemplu: x 2 + x - 20. Pentru a găsi primele monoamele, uita-te la primul membru trinomial și pune-l pe o serie de factori simpli. În acest exemplu, astfel de factori sunt "x" și "x", deoarece x = x * x 2.

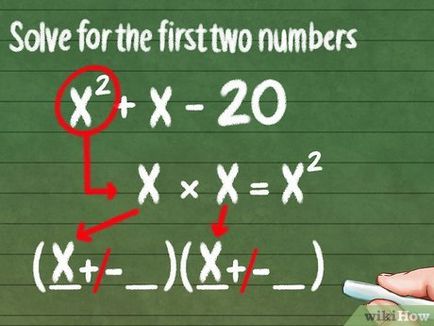
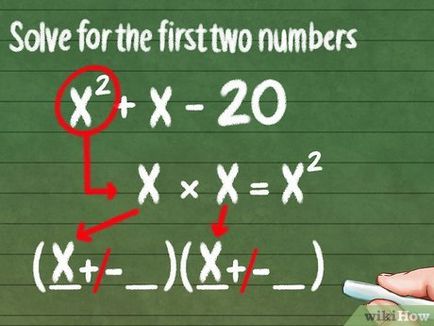
• S-au găsit monoamele Substitut primele lacune în cadrul fiecărei perechi de paranteze: (x + / -__) (x +/- __)
• Amintiți-vă că pătrat - este orice variabilă sau constantă, înmulțită cu ea însăși.

Găsiți două numere al căror produs este egal cu al treilea termen al trinomul. Pentru a face acest lucru, uita-te pentru un al treilea membru al trinomul și răspândirea-l la toate perechile posibile de factori. În exemplul nostru (al treilea membru - acest număr -20) perechi astfel de factori sunt următoarele numere:

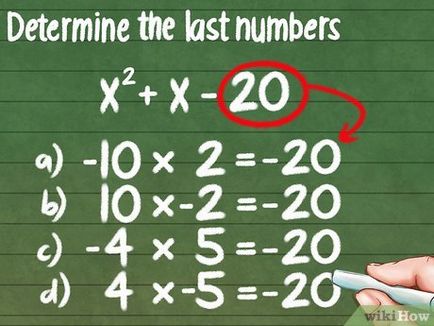
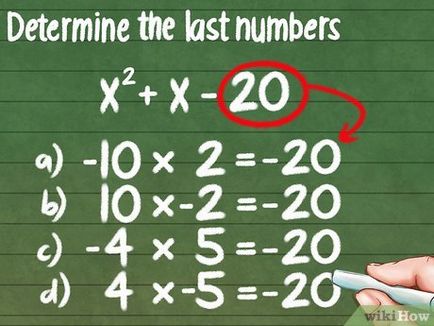
• -10 * 2 = -20
• 10 * -2 = -20
• -4 * 5 = -20
• 4 * -5 = -20
• Rezolvarea polinoame complexe, puteți utiliza zecimale (-3 * 6.6666), dar astfel de polinoame este foarte greu de rezolvat, deoarece este practic imposibil să se aplice metoda de încercare și eroare. În astfel de cazuri, utilizați un calculator de grafică.

Printre găsit (în pasul anterior) perechile de factori, alege o pereche de numere, cu adaos care transforma al doilea termen al trinomul. Permanent (constant) este întotdeauna în fața variabilei. În acest exemplu, al doilea termen al trinomul - este „x“. Deoarece constanta nu este specificat, atunci este egal cu 1, deoarece x * 1 = x. Astfel, este necesar să se aleagă o pereche de numere, care se obține atunci când se adaugă 1. În exemplul, o pereche de numere sunt 4 și 5: -4 + 5 = 1. Astfel, binomi produse vor fi: (x-4) (x + 5).

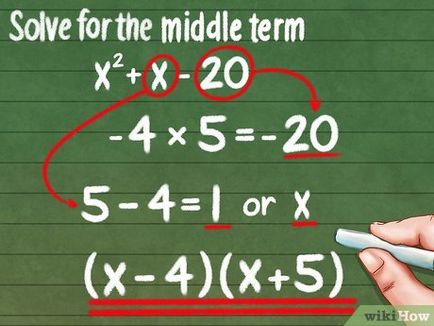
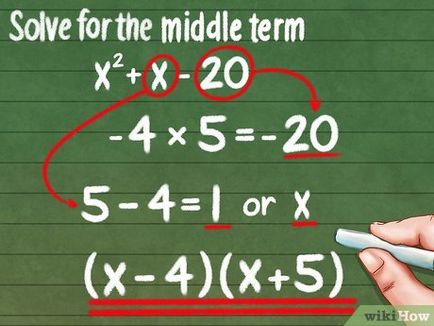
• Numerele pozitive sunt identificate cu plus, și negative - cu scădere.
• Notă. Luați în considerare constanta a primului termen al trinomul. De exemplu, dacă în acest exemplu, primul membru va trinomial 3x 2. o astfel de trinomial nu se descompune în factori (3x-4) (x + 5), deoarece în acest caz, suma rezultatelor bucăților de primul și al doilea și primul și cel de-al doilea element nu este egal cu 1: 15 + (-4) = 11. Aici selectați o altă pereche de multiplicatori -20.

Înmulțiți membrii binomi pentru a verifica rezultatul. În exemplul nostru:

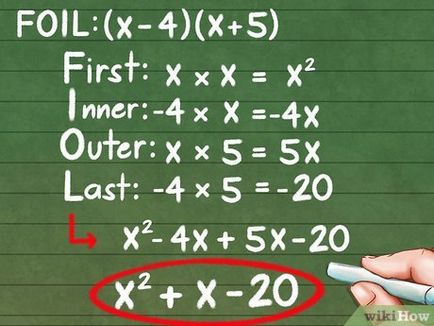
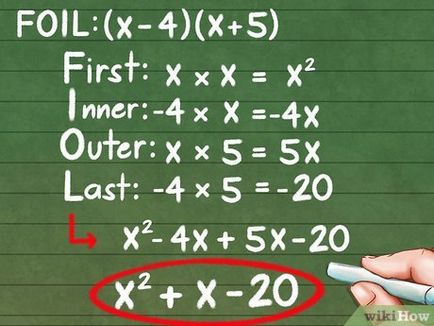
• (4-x) (x + 5)
• Primii membri. x * x = x 2
• Primul și al doilea termen. x * 5 = 5x
• În al doilea rând și primii membri. * X = -4 -4H-
• Al doilea termeni. -4 * 5 = -20
• Ori rezultatele pentru a obține un polinom: x 2 + 5x - 4x - 20
• Fold sau scade alți termeni asemănători: x 2 + x - 20
• Deoarece un trinom obținut coincide cu soluția sursă este corectă.

Practica in factoring trinomials expansiune. Unii trinomial mai dificil să se stabilească decât altele. Încercați să factor următoarele polinomul pătratică și compară răspunsurile la cele ce urmează.

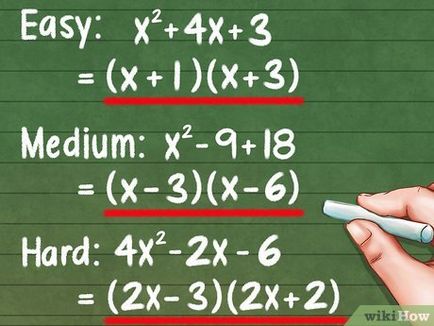
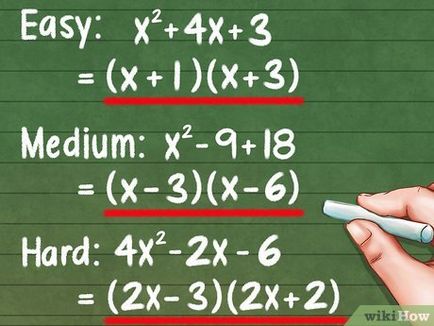
• problemă simplă: x 2 + 4x + 3.
  • Răspuns: (x + 1) (x + 3)
• Ca de obicei problema: x 2 - 9 + 18.
  • Răspuns: (x-3) (x-6)
• O sarcină dificilă: 4x 2 - 2x -6
  • Răspuns: (2x-3) (2x + 2)

Pentru a rezolva un polinom, este necesar de a egala cu zero. Sarcinile necesare pentru a „găsi valoarea unei variabile, pentru care polinomul este 0“ sau „găsi rădăcinile polinomului“ sau pur și simplu „rezolva polinom“. Înainte de polinomul echivalate la zero, urmați sfaturile stabilite în prima secțiune a acestui articol. Să considerăm un exemplu: 3x (2x - 4) (x + 5) = 0.

• „Roots“ polinom situat acolo unde este zero, adică punctele (pe un plan de coordonate), în care un grafic funcție polinomială intersectează axa X (axa orizontală).

Echivala fiecare binom (dacă ați stabilit un polinom de factoring) la zero. Deoarece polinomul este descompus în mai mulți factori, sarcina principală este împărțită în mai multe sub-sarcini. În cazul în care 0 este multiplicată cu orice expresie sau un număr, veți obține un 0, astfel încât să putem lua în considerare fiecare factor separat. Astfel, în exemplul nostru, problema este împărțită în trei subactivități:

• Ecuația A: 3x = 0
• Ecuația B: 2x - 4 = 0
• Din ecuația: x + 5 = 0

Rezolva toate ecuațiile, adică, găsiți „x“. Fiecare soluție va fi rădăcina polinomului originale. Pentru a găsi „x“, obosobte această variabilă pe de o parte a ecuației.

• Ecuația A: 3 lichidează prin următoarea divizare: 3x / 3 = 0/3.
  • x = 0
• Ecuația B: 2x - 4 4 = 0 + 4
  • 2x / 2 = 4/2
  • x = 2
• Ecuația C: x + 5 - 5 = 0 - 5
  • x = -5
• Vei găsi rădăcinile polinomului.

Pentru a verifica răspunsul, substitui valorile găsite în polinomul original. Aceasta este o modalitate rapidă și de încredere pentru a testa orice soluție. În loc de „x“, substituie valorile găsite - în cazul în care decizia este corectă, polinomul va fi egal cu 0.

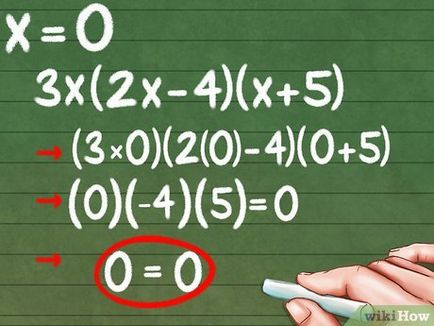
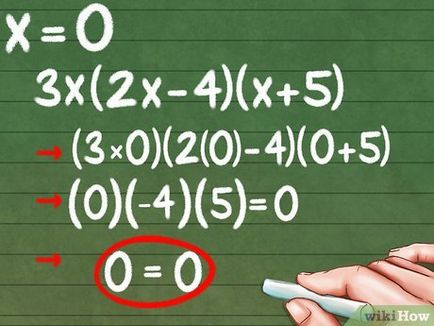
• x = 0: (3 * 0) (2 * 0 - 4) (0 - 5) = 0
  • (0) (- 4) (- 5) = 0
  • 0 = 0
• Corect. Verificați valoarea „x“ rămasă.

Simplificarea polinomul. Pentru a face acest lucru, se pune pe produsul binomului și trinomul. De exemplu, produsul (x-5) (x 2 + x - 20) poate fi împărțită în două ecuații și rezolvarea acestora în mod individual.

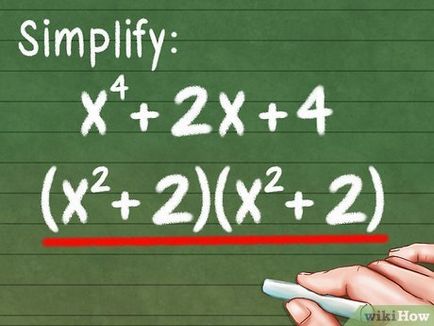
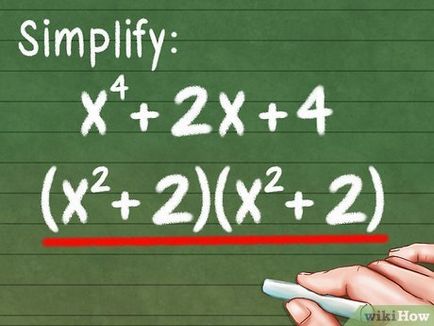
• Fiind dat un polinom de grad mai mare, de exemplu, x 4. poate fi scris ca: (x 2) 2. simplifica în mod considerabil soluția.
  • De exemplu, x 4 + 2x 2 + 4 = (x 2 + 2) (x 2 + 2)

Rezolva polinomială, care este dat ca diferența dintre două cuburi. Dacă numărul de variabile cubic sau cub se scade din alt număr sau variabil, de exemplu, x 3 - 8, atunci această diferență poate fi descompus într-un produs de înmulțire formula Acronim binom și trinomial: (ab) (a 2 + ab + b 2) = 3 - b 3

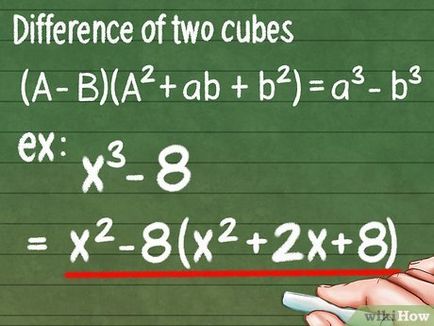
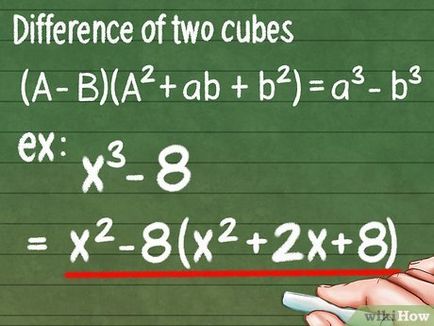
• În acest exemplu, a = x, b = 2 (pentru 2 3 = 8). Prin urmare, x 3 - 8 = (x - 2) (x 2 + 2x + 8).
• Pentru a înțelege modul în care este derivat această formulă, accesați această pagină (în limba engleză).

Aflați cum să rezolve o ecuație pătratică. ecuația pătratică - acesta este un polinom de gradul al doilea, echivalat cu zero. ecuația de gradul doi pot fi folosite pentru a rezolva polinoame complexe fără calculator grafice. Cu ajutorul formulei de rezolvare a unei ecuații pătratice, puteți găsi rapid rădăcinile polinomului.