Cum de a găsi domeniu și gama de valori ale funcției

Fiecare funcție are două variabile - variabila independentă și variabila dependentă, ale cărei valori depind de valorile variabilei independente. De exemplu, o funcție y = f (x) = 2x + y variabilă independentă este "x" și dependent - "y" (cu alte cuvinte, "y" - este o funcție de "x"). Valorile valide sunt independente „x“ variabilă este numit domeniul functiei, iar valorile valide pentru variabila dependentă „y“ se numește domeniul valorilor. [1]

pași Editare

Partea 1 din 3: Găsirea domeniul functiei Edit

Se determină tipul de caracteristicile de care aveți nevoie. Valorile din zona de toate valorile valide sunt „x“ (reprezentate grafic pe axa orizontală), care corespund valorilor valide „y“. Funcția poate fi pătrată sau conțin fracțiuni sau rădăcini. Pentru a găsi domeniul funcției trebuie să determine mai întâi tipul de funcții.

• Functia pătratic are forma ax 2 + bx + c: [2] f (x) = 2x 2 + 3x + 4
• Funcția conținând fracția: f (x) = (1 / x), f (x) = (x + 1) / (x - 1) (și așa mai departe).
• Funcția care conține rădăcină: f (x) = √x, f (x) = √ (x 2 + 1), f (x) = √x (și așa mai departe).

Selectați intrarea corespunzătoare pentru domeniul funcției. Domeniul definiției este scris într-un pătrat și / sau paranteze rotunde. Un suport pătrat este utilizat în cazul în care valoarea este în domeniul funcției; în cazul în care valoarea nu este inclusă în domeniu, utilizați paranteze. În cazul în care are mai multe zone non-contigue de definiție, între ele a pus simbolul «U». [3]

• De exemplu, domeniul [-2,10) U (10,2] include valorile -2 și 2, dar nu include valoarea 10.
• Cu simbolul ∞ infinit folosiți întotdeauna între paranteze.

Construirea unui grafic al unei funcții pătratică. Graficul acestei funcții este un parabole ale cărui ramuri sunt îndreptate fie sus sau în jos. Deoarece parabola crește sau scade de-a lungul axei X, domeniul de definire a funcției pătratice sunt toate numerele reale. Cu alte cuvinte, domeniul de o astfel de funcție este un set de R (R reprezintă toate numerele reale). [4]

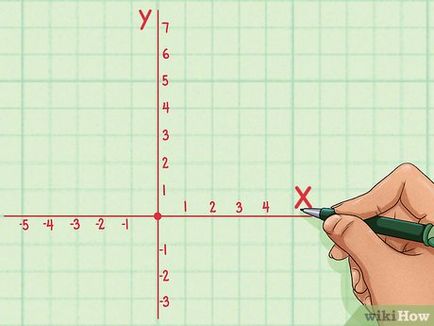
• Pentru o mai bună înțelegere a conceptului de funcție, selectați orice valoare de „x“, înlocuiți-l într-o funcție și pentru a obține valoarea „y“. O pereche de valori „x“ și „y“ reprezintă un punct de coordonate (x, y), care se află pe graficul funcției.
• Aplicați acest punct pe planul de coordonate și de a efectua procesul de mai sus, cu o valoare diferită de „x“.
• Inflicting pe planul de coordonate câteva puncte, veți obține o idee de forma funcțiilor graficului.

Dacă funcția conține o fracție, numitorul egalează-l la zero. Amintiți-vă că nu vă puteți împărți cu zero. Prin urmare, echivalând numitorul la zero, veți găsi valoarea „x“, care nu fac parte din domeniul funcției. [5]

• De exemplu, pentru a primi domeniul funcției f (x) = (x + 1) / (x - 1).
• Aici, numitorul (x - 1).
• Echivala numitor la zero și pentru a obține 'x' x - 1 = 0; x = 1.
• Înregistrează domeniul funcției. Domeniul definiție nu include 1, adică include toate numerele reale cu excepția 1. Astfel, domeniul funcției: (-∞, 1) U (1, ∞).
• Record (-∞, 1) U (1, ∞) are următorul conținut: mulțimea tuturor numerelor reale, cu excepția 1. Simbolul ∞ infinit este toate numerele reale. În exemplul nostru, toate numerele reale, care este mai mare de 1 și mai puțin de 1, inclus în definiția.

Dacă funcția conține rădăcina pătrată, radicand trebuie să fie mai mare sau egală cu zero. Amintiți-vă că rădăcina pătrată a unui număr negativ nu poate fi ejectat. Prin urmare, orice valoare de „x“ în cazul în care radicand este negativ, este necesar să se excludă din domeniul funcției. [6]

• De exemplu, pentru a primi domeniul funcției f (x) = √ (x + 3).
• Expresia radicală: (x + 3).
• Radicand trebuie să fie mai mare sau egală cu zero: (3 + x) ≥ 0.
• Caută "x": x ≥ -3.
• Domeniul acestei funcții include un set de toate numerele reale mai mari sau egale cu -3. Astfel, definiția de suprafață: [-3, ∞).