Cum de a calcula volumul unei piramide pătrat

Pătrat piramidă - formă volumetrică cu o bază în formă de pătrat și marginile laterale triunghiulare. Vârful piramidei pătrat este proiectată în centrul bazei. Dacă „o“ - parte a bazei pătrate, «h» - înălțimea piramidei (perpendiculara a scăzut de la vârful piramidei la centrul bazei sale), atunci volumul unei piramide pătrat poate fi calculat prin formula: a 2 x (1/3) h. Această formulă este valabilă pentru orice dimensiune de piramide pătrate (de la piramide suveniruri la piramidele egiptene).

pași Editare

Metoda 1 de la 2:
Calcularea volumului zonei și înălțimea Edit

Găsiți partea laterală a bazei. Deoarece baza piramidei pătrat este un pătrat, toate bazei egale. Prin urmare, este necesar să se găsească lungimea oricărei laturi a bazei.

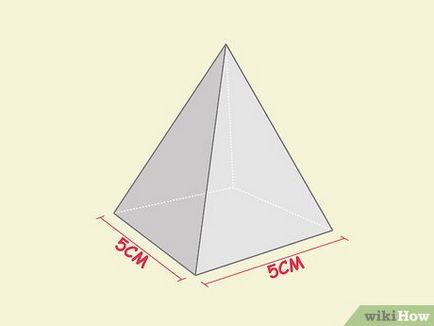
• De exemplu, având în vedere latura bazei piramidei, care este egală cu 5 cm.
• În cazul în care părțile laterale ale bazei nu sunt egale între ele, atunci vi se oferă o formă dreptunghiulară, mai degrabă decât o piramidă pătrată. Cu toate acestea, formula de calcul a volumului piramidei dreptunghiulare este similar cu formula de calcul a volumului unei piramide pătrat. Dacă «l» și «w» - două adiacente (inegale), în partea de jos a piramidei dreptunghi, volumul piramidei calculat prin formula: (l x w) x (1/3) h

Se calculează suprafața de bază pătrată, înmulțind partea sa pe sine (sau, cu alte cuvinte, direcția de ridicare într-un pătrat).

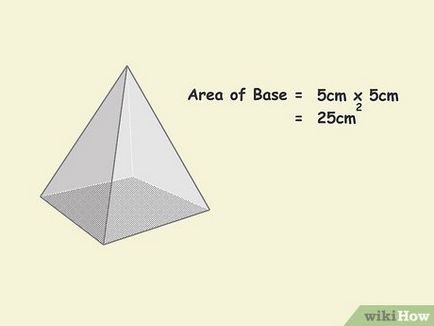
• In exemplul nostru, 5 x = 5 5 2 = 25 cm2.
• Nu uitați că zona este măsurată în unități pătrate - centimetri pătrați, metri pătrați, kilometri pătrați, și așa mai departe.

Înmulțiți zona bazei la înălțimea piramidei. Înălțimea - perpendiculara a scăzut de la vârful piramidei de pe baza sa. Prin multiplicarea acestor valori, veți obține un volum de un cub cu aceeași bază și înălțime ca și cea a piramidei.

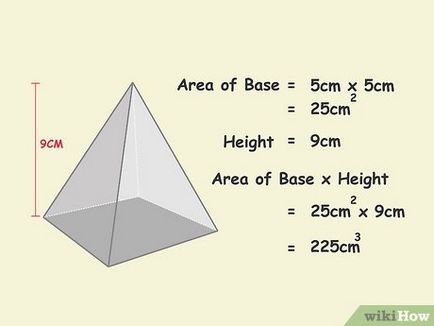
• În acest exemplu, înălțimea este de 9 cm 25 cm 2 cm x 9 cm 3 = 225
• Nu uitați că volumul este măsurat în unități cubice, în acest caz, în centimetri cubi.

Împărțiți rezultatul de 3 și veți găsi volumul unei piramide pătrat.

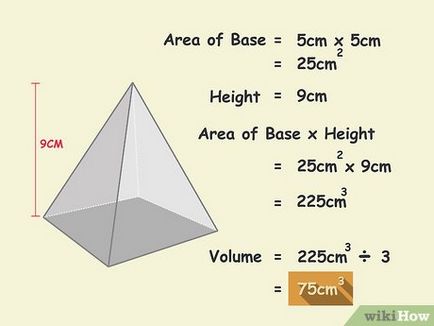
• În acest exemplu, 225 cm 3/3 = 75 cm3.
• Volumul este măsurat în unități cubice.

Metoda 2 din 2:
Calcularea volumului apotemă Editare

Dacă vi se administrează fie aria sau înălțimea piramidei și apotemă sale, puteți găsi volumul unei piramide, folosind teorema lui Pitagora. Apotemă - este înălțimea teșiturile triunghiulare ale piramidei, extrase din vârfurile triunghiului la baza sa. Pentru a calcula apotemă utiliza partea laterală a bazei piramidei și înălțimea acesteia.

• Apotemă împarte latura bazei în jumătate și taie-l în unghi drept.

Luați în considerare un triunghi format din dreapta înălțime apotemă și segmentul care leagă centrul bazei și mijlocul mâinii sale. Acest triunghi este apotemă ipotenuzei, care poate fi găsit pe teorema lui Pitagora. Segment care leagă centrul bazei și partea ei de mijloc, este egală cu jumătate din latura de bază (acest segment este unul dintre picioare, piciorul este a doua înălțime a piramidei).

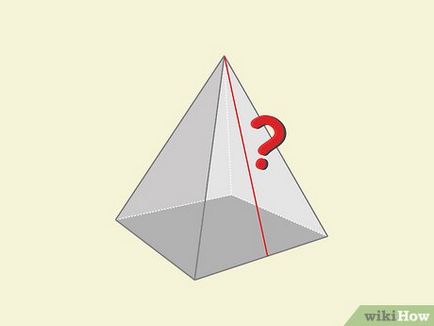
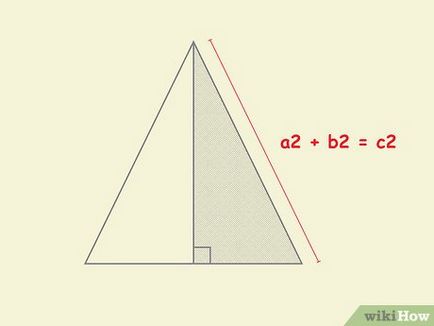
• Să ne amintim că teorema lui Pitagora poate fi scris ca: a 2 + b 2 = c 2. în cazul în care «a» și «b» - picioare, «c» - ipotenuza unui triunghi dreptunghic.
• De exemplu, având în vedere o piramidă a cărei latură de bază este de 4 cm și apotemă - 6 cm, în scopul de a găsi înălțimea piramidei, substituie aceste valori în teorema lui Pitagora ..
  • a 2 + b 2 = c 2
  • un 2 + (4/2) 2 = 6 2
  • un 2 = 32
  • a = √32 = 5,66 cm Găsești a doua etapă a unui triunghi dreptunghic, care este înălțimea piramidei (apotemă, de asemenea, în cazul în care s-ar fi dat și înălțimea piramidei, ai putea găsi jumătate din baza piramidei).

Utilizați valoarea găsită pentru a găsi volumul piramidei prin formula: o 2 x (1/3) h.

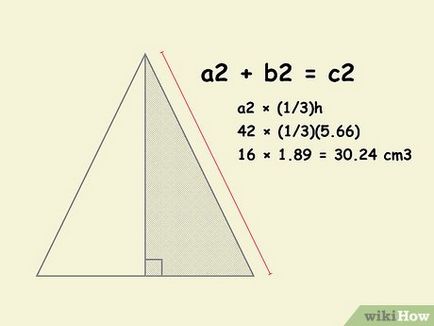
• În exemplul nostru, ați calculat că înălțimea piramidei este de 5,66 cm, valorile de substituție în formulă pentru a calcula volumul piramidei .:
  • un 2 x (1/3) h
  • 02 aprilie × (1/3) (5,66)
  • 16 x 1,89 = 30,24 cm3.

Dacă vi se administrează apotemă, utilizați marginea piramidei. Rib - un segment care leagă vârful piramidei cu vârful pătrat, la baza piramidei. În acest caz, veți obține un triunghi dreptunghic, picioarele care sunt înălțimea piramidei și jumătate diagonală de pătrat la baza piramidei, iar ipotenuza - marginea piramidei. Deoarece diagonala pătrat este egală cu √2 × parte a pieței, puteți găsi o parte a pieței (e) pentru împărțirea diagonală la √2. Apoi, va fi capabil să găsească volumul unei piramide formula de mai sus.

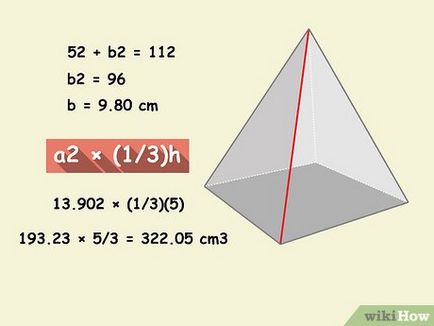
• De exemplu, având în vedere o piramidă pătrată având o înălțime de 5 cm și 11 cm margine calculează jumătate diagonală urmează .:
  • Mai 2 + b 2 = 11 2
  • b 2 = 96
  • b = 9,80 cm.
  • Ai găsit jumătate în diagonală, astfel încât diagonala este egală cu: 9,80 cm x 2 = 19,60 cm.
  • o latură pătrată (de bază) este egal cu √2 × diagonală, deci 19,60 / √2 = 13,90 cm Acum afla volumul piramidei prin formula :. a x (1/3) h 2
  • 13.90 2 x (1/3) (5)
  • 193,23 x 5/3 = 322,05 cm 3