Cifrele regulate si corp - studopediya

„Pitagora a transformat geometria, dându-i forma unei științe libere, având în vedere principiile sale mod pur abstract și explorarea teorema cu intangibile și punct de vedere intelectual. El a fost cel care a descoperit teoria numerelor și structura corpurilor cerești iraționale ". Deci, în valoare contribuția la geometria pitagoreice Proclu și această estimare filosof antic pe buna dreptate.

De fapt, geometria pitagoreică școală într-o disciplină științifică independentă. A fost Pitagora și adepții săi au fost primii pentru a studia sistematic geometria - ca o doctrină teoretică a proprietăților forme geometrice abstracte, mai degrabă decât ca o colecție de rețete aplicate de către un geometru. În acest caz, cel mai important, proprietățile figuri geometrice pitagoreice care nu este stabilită prin măsurarea în timp ce folosind o dovadă logică.

Cu cel mai larg domeniu de aplicare practică, geometria primelor învățăturile pitagoreana # 956; # 940; # 952; # 951; # 956; # 945; El a aruncat un văl de „secret“ și a devenit cel mai popular știință. Cu toate acestea, în „Viața lui Pitagora“ Iamblichus motive pentru popularitatea geometriei prezentate oarecum diferit: „Acesta este modul în care pitagoreici explica de ce geometria a devenit accesibilă publicului. A fost vina unuia dintre ei, care și-a pierdut bani comunitățile pitagoreice. După această comunitate dezastru a permis ca el să câștige bani cu ajutorul geometriei - geometria se numește „Tradiție pitagoreică.“ Având în vedere faptul că, în V. BC. e. Ei au fost foarte populare sofiștii - profesor itinerant de înțelepciune, este foarte posibil ca pitagoreici nu a ezitat să umple cuferele de predare.

Astfel, datorită Hipocrate din Chios, avem motive să credem că pitagoreici, în general, a construit întreaga planimetrie formele rectilinii. Ei au studiat proprietățile de triunghiuri, dreptunghiuri, paralelograme, trapeze, sa dovedit o teoremă despre suma unghiurilor de triunghiuri, teorema de pe partea laterală a triunghiului, care se află în unghiul obtuz, al egalității teoremei pe triunghiuri. Vârful geometriei plane figurilor rectilinii a fost o dovadă a celebrului teorema lui Pitagora. Aceste rezultate geometria pitagoreică, se pare, și am format baza cărții „Elemente“ a lui Euclid, care se termină teorema lui Pitagora.

Pitagoreicii au manifestat interes în cifrele și organismele corecte a crescut. forme geometrice regulate din cauza lor „corectă“, adică. E. Prezența sau oglindă rotativă (și de multe ori unul sau altul) de simetrie, precum și posibil pe parcursul întregii răspunde pitagoreice la un regulat, ordonat structural structura armonică a universului. (Acest aspect ne vom întoarce la nr. 2.2 și 4.3.) Forma geometrică, în special în dreapta, a relevat cel mai impresionant numărul și nu ar putea fi mai potrivite pentru a „extrage o serie de lucruri.“ a pus pitagoreice una pe celelalte forme geometrice (de obicei, pe dreapta sau „purtător“ orice număr de „sfinți“) și că realizarea vizibilă a fenomenelor de coerență.

Acesta este motivul pentru care pitagoreici a acordat o importanță deosebită pentru ei a demonstrat teorema că un avion poate fi complet (de exemplu, nu „găuri“, și suprapuneri ..) pentru a acoperi doar trei poligoane regulate: triunghiuri, patrate si hexagoane (Figura 42.). Dovada acestei teoreme este destul de transparentă, și am lăsa cititorului. Nu este dificil și construirea cifrele corecte, iar cifrele derivate din acestea prin dublarea partile laterale.

Dar acum construirea unui pentagon regulat nu mai este atât de evidentă. Noi nu știm cum să construiască un pentagon regulat pitagoricieni. Dar se știe că steaua cu cinci colțuri - principala marca de simbol și de identificare - acestea sunt formate din trei triunghiuri isoscele. Acest ecou în mod clar metoda de construire a unui pentagon regulat, descris de Euclid ( "Elements", Vol. IV, prev. 11). Așa că metoda lui Euclid, probabil, datează din pitagoreici. Consideră-l.

Având în vedere un cerc înscris într-un triunghi isoscel ACD. care. (Metoda de construire astfel de triunghi indicăm în cap. 2.2.) Și desena un bisectoare CE DB unghiurile C și D, respectiv. Apoi colțurile 1 - 5 (. Figura 43) sunt egale și, prin urmare, va fi egală cu arcul corespunzător și înăsprirea corzii, adică ... Deci, înscris în cercul ABCDE fi un pentagon echilateral. Deoarece ambele unghiuri, bazate pe același arc AB și AE, respectiv, toate unghiurile 1 - 7 sunt egale și, în consecință, fiecare colț al pentagonului ABCDE va ​​fi compusă din trei unghiuri egale, adică ... Astfel construit pentagon este echilateral și equiangular, t. E. Be.

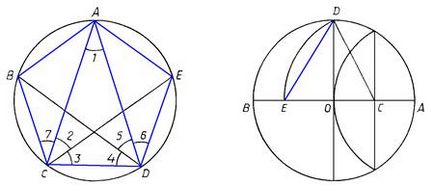
De-a lungul timpului, matematicianul grec a fost găsit un mod mai ușor de a construi un pentagon regulat. Acesta este descris într-o altă antichitate compoziție remarcabilă - „Almagest“ Ptolemeu (circa 150), care, la fel ca „începutul“ geometriei euclidiene, o enciclopedie a cunoașterii antice de astronomie. Ptolemeu împarte în jumătate raza cercului OA (C dot) și CD-ul descrie o rază de cerc la intersecția cu diametrul AB la punctul E (fig. 44). Apoi ED este partea unui pentagon regulat. (Dupa ce a citit paragraful. 2.2 Cititorul poate dovedi cu ușurință singur.)

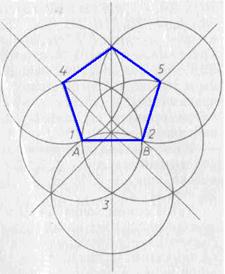
După un alt mileniu și jumătate, în 1525 Albreht Dyurer (1471-1528), un pictor și om de știință, unul dintre titanii Renașterii, în tratatul său „Ghid pentru măsurarea cu rigla și compasul“ au o metodă aproximativă de construire a unui pentagon regulat pe o anumită parte AB cu folosind compasul "ruginit", t. e. o singură soluție caliper. Metoda Dürer clar din Figura 45, în care numerele de busolă picioare au fost identificate în mod constant. Metoda Dürer diferă de mare precizie (unghiuri 1 și 2 nu sunt egale cu 108 °, o. Unghiuri 4 și 5 puțin mai mare de 107 °, în timp ce unghiul C puțin mai mult de 109 °), astfel încât erorile sale în ochi nu este complet perceput. Dürer însuși a făcut nici o mențiune cu privire la natura aproximativă a construcțiilor lor, probabil, considerîndu-le să fie corecte. Cu toate acestea, metoda de Durer este aproximativă. (Încearcă să-l dovedească.)

Și cum să construiască cu ajutorul unui conducător și busola după figura corectă - Heptagon? Această sarcină a fost descurajantă nu numai vechi pitagoreici, dar a rămas nerezolvată pentru mai mult de două milenii! Numai în 1796, în vârstă de 19 ani, băiat german Carl Friedrich Gauss (1777-1855), supranumit regele mai târziu matematicieni a rezolvat-o. Gauss a arătat că problema de a construi o riglă și compas corect-n gon, este echivalentă cu problema împărțirea cercului în n părți egale, este asociat cu rădăcinile studiului. Mai mult, Gauss a demonstrat că regulate N-Gon pot fi construite prin rigla și compasul dacă și numai dacă N - prim de forma

numere prime de forma (2.1.1), se face referire la numărul de ferme, și încă mai știu doar cinci dintre aceste numere :.

Acest rezultat Gaussian generalizează la cazul în care numărul de laturi ale poligonului n este produsul numerelor de forma (2.1.1). Având în vedere, de asemenea, posibilitatea de dublare n. Formulăm teorema Gauss. poligon regulat pot fi construite folosind busola și rigla dacă și numai dacă numărul de laturile sale are forma

De fapt. din moment ce alte numere Fermat este încă necunoscut.

Este ușor de observat că toate poligoanele care au putut să construiască grecii antici, și anume cei care au. conținute în (2.1.2). Astfel, prin adăugarea de noi poligoane antice cu n = 17, 34, 51, 68, 85, 126, 252, 255 și 257. Noul principiu acestea sunt 17-gon-gon 257 și 65 537 gon. Gauss a găsit o metodă de construcție a primelor două poligoane. Rețineți că descrierea metodei de construcție a 257-gon Gauss a durat aproximativ cincizeci de pagini. Gauss durata de viață este extrem de mândru de descoperirea lui tineresc și lăsat moștenire gravat pe mormântul său obișnuit de 17-Gon înscris într-un cerc.

Astfel, un poligon regulat construi rigla și compasul posibile atunci când n = 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 32, 34, .... nu se poate, atunci când n = 7, 9, 11, 13, 14, 18, 19, 21, 22, 23, 25, 26, 27, 28, 29, 30, 31, 33.

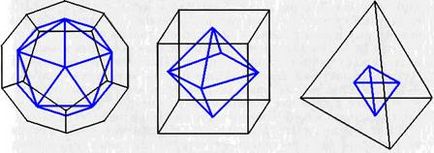
Ne întoarcem acum la poliedre regulate. Există doar cinci, și Proclu în afară de descoperiri remarcabile în geometria plan Pitagora îi atribuie construirea a cinci solide regulate. Astăzi, cu toate acestea, matematicieni, istoricii preferă să nu cred blestemat, și a găsit scolie (# 963; # 967; # 972; # 955; # 953; # 959; # 957; - interpretare, explicația) în cartea XIII "elemente" ale lui Euclid, în cazul în care se spune, Pitagora știa doar trei corpul corect - tetraedru, hexaedru (cub) și dodecaedrul, iar mai târziu a deschis Theaitetos, iar celelalte două - octaedru și icosaedru. În acest lucru și într-un alt caz, dovezile antice ne spune despre interesul pitagoreici organismelor corecte.

Se pare că natura însăși a determinat pitagoreici forma de telefon regulate: cristale de sare au o forma unui cub, alaun - octaedru, si cristale de pirita - dodecaedrul. În sfârșit, după cum arată săpăturile din Italia, a fost un favorit de copii de jucărie etrumynskih în timpul lui Pitagora.

Numele unui poliedru regulat este dată de numărul de marginile sale (de exemplu, un tetraedru - # 964; # 949; # 964; # 961; # 940 - # 949; # 948; # 961; # 959; # 957; - # 964; # 949; # 964; # 961; # 940; # 962; - chetype + # 949; # 963; # 961; # 945; - o zonă a corpului, fata - un tetraedru). poliedre regulate sunt prezentate în Figura 46, iar caracteristicile lor geometrice sunt rezumate în Tabelul, unde m reprezintă numărul de fețe la vârful.

Pitagoreicii observat că cubul numărul de noduri (8) este media armonică a numărului de fețe (6) și numărul de nervuri (12) și, prin urmare, este numit corpul armonic cubică. cub misiune specială a fost văzută, de asemenea, în faptul că el a fost singurul solide regulate umple complet spațiul.

La momentul Euclid, sa observat că cub octaedru, dodecaedrul și icosaedru sunt duale (dublă), t. E. Numărul de fețe ale corpului egal cu numărul de vârfuri ale celuilalt și viceversa. Apoi, un corp poate fi obținută de cealaltă dacă centroizii fețele de a accepta noduri pentru celălalt sau invers (fig. 46). Tetraedru este dublă pentru sine.

Cu toate acestea, cea mai importantă proprietate a poliedre convexe a fost găsit doar în mijlocul secolului al XVIII-lea. Teorema lui Euler. în orice număr de vârfuri ale unui poliedru convex (L) plus numărul de fețe (M) minus numărul de aripioare (N) este o valoare constantă egală cu două:

Și totuși, caracteristica cea mai intrigant de solide regulate, este că ele există doar cinci. Nu întâmplător dovada acestui fapt a fost realizat ultima XIII carte „elemente“ ale lui Euclid. [44] De fapt, cantitatea de avion S la unghiurile de vârfuri ale unui poliedru convex trebuie să fie strict mai mic de 360 ​​°, în timp ce numărul de fețe la vârful. Deci, se confruntă solide regulate pot fi doar trei poligoane regulate: un triunghi, pătrat, pentagon, hexagon, deoarece chiar și pentru. puteți face trei corpul corect de triunghiuri echilaterale: - tetraedrul - octaedru și - un icosaedru (cu). De pătrate și pentagonale regulate - doar un singur (cub și dodecaedrul), atunci când (în cazul în care - pentru piețele și - pentru pentagoane). Astfel, poliedre regulate poate fi doar cinci.

Acest fapt nu a putut rămâne indiferentă predispuse la misticism numerică a pitagoreici, și în spatele lor, Platon și neoplatonicilor. Platon a dezvoltat faimoasa doctrina „elemente“, cele cinci - baza universului, atomii din care este conceput sub formă de solide regulate. (Mai mult Platon această doctrină va fi discutată în alin. 4.3.) De atunci, poliedre regulate este adesea numit solide platonice.

poliedre regulate de-a lungul istoriei omenirii nu încetează să admire simetria minților iscoditoare, înțelepciunea și perfecțiunea formelor sale. Leonardo da Vinci a iubit meșterit schelete solide regulate, și să le prezinte ca un cadou aristocrației, probabil, într-o încercare de a atașa puterile care să fie la reflecția filosofică asupra frumuseții adevărurilor eterne (fig. 47).

Fig. 47. Desene de modele de lemn ale dodecaedrul și icosaedru, realizat de Leonardo da Vinci pentru o carte prietenului său Luca Pacioli „Pe Proporția divină.“ Veneția. 1509

Fig. 48. Fig. 49. Al șaptelea organism Arhimede în formă de stea - icosidodecahedron.