Basic (de bază) și un drum liber variabile (non-core)

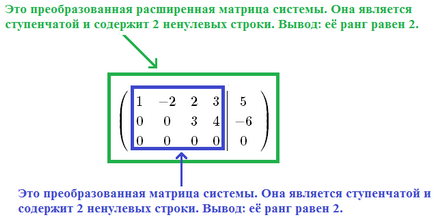
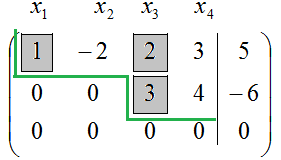
Tema „Kronecker-Capelli Teorema“, sa afirmat că în cazul în care gradul de expansiune sistem matrice $ \ widetilde $ rang și sistemul de matrice $ A $ sunt egale, atunci dat sistemul de ecuații algebrice liniare (SLAE) compatibil, adică Ea are o soluție. Problema cu privire la numărul de soluții care au fost activate investigarea Kronecker. Potrivit lui, în cazul în care $ \ A sunat = \ sunat \ widetilde = n $ ($ n $ - număr necunoscut), care Slough are o soluție unică. Dacă $ \ A sunat = \ sunat \ widetilde

De interes special este cazul $ \ A sunat = \ sunat \ widetilde

Ce înseamnă expresia „rangul este egal cu $ r $“? Aceasta înseamnă că există cel puțin un minor $ r $ lea ordin, care nu este zero. Îmi aduc aminte că un minor se numește bază. Baza minorilor pot fi mai multe. Astfel, toți minorii a căror ordine este peste $ r $, sunt egale cu zero sau nu există.

În cazul în care coeficienții variabilelor $ r $ formează împreună SLAE sistem bază de matrice minoră $ A $, atunci aceste variabile $ r $ numit de bază sau fundamentală. Restul de $ n-r variabilele $ numite liber sau non-core.

$ R $ Selectați variabilele de bază, în general, poate fi o varietate de moduri. În exemplele voi arăta cel mai frecvent folosit metoda de alegere.

Soluție Slough. în care toate variabilele libere sunt zero, numit de bază.

In toate exemplele de mai jos, sistemul de matrice este notat cu $ A $, iar matricea augmented a sistemului - scrisoarea $ \ widetilde $.

Rezolva sisteme liniare \ $ din stânga \<\begin & 3x_1-6x_2+9x_3+13x_4=9\\ & -x_1+2x_2+x_3+x_4=-11;\\ & x_1-2x_2+2x_3+3x_4=5. \end \right.$. Если система является неопределённой, указать базисное решение.

Deci, avem sisteme liniare, care are 3 ecuații și 4 variabile: $ x_1 $, $ x_2 $, $ x_3 $, $ x_4 $. Pe măsură ce numărul de variabile este mai mare decât numărul de ecuații, un astfel de sistem nu poate avea o soluție unică (un pic mai târziu vom demonstra strict propunerea pe baza Kronecker-Capelli). Slough găsi soluții folosind Gauss:

$$ \ stânga (\ începe 3 -6 9 13 9 \\ -1 2 1 1 -11 \\ 1 -2 2 3 dreapta) \ rightarrow \ left 5 \ end \ | \ începe \ Text \\ \ Text \\ \ Text \ end \ dreapta | \ Rightarrow \\ \ rightarrow \ stânga (\ începe 1 -2 2 3 5 \\ -1 2 1 1 -11 \\ 3 -6 9 13 9 \ end \ dreapta) \ începe \ fantomă \\ II + I \\ III-3 \ cdot I \ end \ rightarrow \ stânga (\ începe 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 3 4 -6 \ end \ dreapta) \ începe \ fantomă \\ \ fantomă \\ III-II \ end \ rightarrow \\ \ rightarrow \ stânga (\ începe 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ end \ dreapta) $$

Am finalizat cursa de avans a metodei Gauss, aducand matricea augmentată a sistemului de a forma esalon. În partea stângă a caracteristicilor sunt elemente ale matricei sistemului transformat, suntem, de asemenea, a condus la eșalonul de formă. Permiteți-mi să vă reamintesc că, dacă dat o anumită matrice pentru a forma Echelon, atunci rangul său este egal cu numărul de rânduri nenuli.

Și matricea sistemului și sistemul de matrice extins după transformări echivalente sunt reduse la forma esalon; Ele conțin două non-zero linie. Concluzie: $ \ A sunat = \ sunat \ widetilde = 2 $.

Astfel, având în vedere SLAE cuprinde patru variabile (notate ca număr $ n $, adică $ n = 4 $). În plus, sistemul ocupă locul sistemului și matricea augmented a matricei sunt egale între ele și egale cu numărul de $ r = $ sau 2. Deoarece $ r

Noi găsim aceste soluții. Pentru a începe, selectați variabilele de bază. Numărul lor ar trebui să fie egală cu $ r $, adică, în cazul nostru, avem două variabile de bază. Ce fel de variabile (pentru că noi le avem 4 bucati) pentru a accepta ca bază? De obicei, variabilele de bază iau acele variabile, care sunt situate pe primele locuri în rândurile nenule ale matricei transformate a sistemului, și anume, pe „pașii“. Ce este acest „pas“ este prezentată mai jos:

Pe „treptele“ sunt numărul de coloane №1 și №3. Prima coloană corespunde variabilei $ x_1 $, iar a treia coloană corespunde variabilei $ x_3 $. Că variabilele $ x_1 $ și $ $ x_3 ia ca bază.

De ce putem accepta variabilele $ x_1 $ și $ $ x_3 ca bază? Pentru a răspunde la această întrebare, să ne amintim că rangul sistemului este numărul de $ r = 2 $. Se spune că toți minorii din această matrice. comandă este mai mare de 2, sau egală cu zero, sau nu există. minori nenuli printre minori au doar un al doilea ordin. Am ales orice ordine nenul al doilea minor. O putem alege ca în matricea originală sistem $ A $, adică, în matricea $ \ left (\ begin 3 -6 9 13 \\ -1 2 1 1 \\ 1 -2 2 3 \ end \ dreapta) $, iar matricea sistemului transformat, și anume, în $ \ left (\ începe 1 -2 2 3 \\ 0 0 3 4 \\ 0 0 0 0 \ end \ dreapta) $. Deoarece matrice de transformare mai multe zerouri sistemul, atunci acesta va lucra cu ea.

Deci, să aleagă a doua comanda elemente minore, care se află la intersecția liniilor №1 și №2, și coloanele №1 și №2:

Concluzie: contactul selectat al doilea ordin minor nu este de bază, pentru că este zero. Deoarece elementele acestui minor este luat din coloana №1 (aceasta corespunde variabilei $ x_1 $) și coloana №2 (aceasta corespunde variabilei $ x_2 $), atunci perechea de variabile $ x_1 $ și $ $ x_2 nu pot fi variabile de bază.

Fa-o a doua tentativă, luând minor elemente de ordinul a doua se află la intersecția liniilor №1, №2 și coloane №2 și №4:

Concluzie: Contactul selectat este o bază minoră de ordinul doi, deoarece nu este zero. Deoarece elementele acestui minor este luat din coloana №2 (aceasta corespunde variabilei $ x_2 $) și coloana №4 (aceasta corespunde variabilei $ x_4 $), un cuplu de variabile x_2 $ $ și $ $ X_4 poate fi luată ca bază.

Hai să facem o a treia încercare de a găsi și valoarea minorului, elementele din care sunt situate la intersecția liniilor №1, №2 și coloane №1 și №3:

Concluzie: Contactul selectat este o bază minoră de ordinul doi, deoarece nu este zero. Deoarece elementele acestui minor este luat din coloana №1 (aceasta corespunde variabilei $ x_1 $) și coloana №3 (aceasta corespunde variabilei $ x_3 $), un cuplu de variabile $ x_1 $ și $ $ x_3 poate fi luată ca bază.

După cum puteți vedea, selecția variabilelor de bază nu este lipsită de ambiguitate. De fapt, numărul de alegeri nu este mai mare decât numărul de plasare de $ n $ elemente $ r $, adică nu mai mult de $ C _ ^ $.

În acest exemplu, așa cum au fost adoptate baisnyh variabile $ x_1 $ și $ x_3 $ - doar pentru motive de comoditate a soluțiilor suplimentare. Ce este această comoditate, vom vedea un pic mai târziu.

Variabilele de bază sunt alese: este $ x_1 $ și $ x_3 $. Restul $ n-r = 2 variabile $ (adică $ x_2 $ și $ x_4 $) sunt gratuite. Trebuie să-și exprime variabilele de bază prin intermediul liber.

Prefer să lucrez cu sistemul în formă de matrice. Pentru a începe Cleanse rezultat matrice $ \ left (\ începe 1 -2 2 3 5 \\ 0 0 3 4 -6 \\ 0 0 0 0 0 \ end \ dreapta) $ de la linia de zero:

$$ \ stânga (\ începe 1 -2 2 3 5 \\ 0 0 3 4 -6 \ end \ dreapta) $$

variabile libere, și anume, $ X_2 $ și $ x_4 $, coloana corespunzătoare №2 și №4. Derularea rapidă înainte aceste coloane peste linie. Conectați-vă toate elementele transportate de coloana se va schimba contrariul:

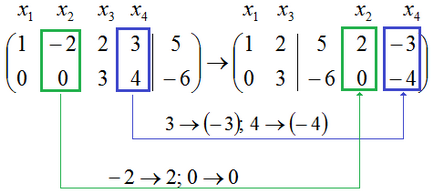
De ce am semne? Ce toate acestea înseamnă transferul de coloane? Afișați \ ascunde

Să ne întoarcem la matricea sistemului extins, care, după transformare este de forma $ \ left (\ începe 1 -2 2 3 5 \\ 0 0 3 4 -6 \ end \ dreapta) $. Să trecem la ecuațiile matricei. Primul rând corespunde ecuației $ x_1-2x_2 + 2x_3 + 3x_4 = $ 5, iar a doua linie corespunde ecuației $ 3x_3 + 4x_4 = -6 $. Acum transfera variabilele gratuite x_2 $ $ și $ $ X_4 pe laturile dreaptă de ecuații. Bineînțeles, atunci când ne deplasăm expresia $ 4x_4 $ în partea dreaptă a ecuației, semnul se va schimba la opusul, iar partea dreaptă va fi de $ -4x_4 $.

\ începe x_1 + 2x_3 = 5 + 2x_2-3x_4; \\ 3x_3 = -6-4x_4. \ end

Dacă din nou pentru a înregistra sistemul rezultat sub forma unei matrice, obținem o matrice cu coloane deplasate peste linie.

Și acum vom continua abordarea metoda obișnuită de Gauss. Scopul nostru: de a face matricea la funcțiile unității. Pentru a începe, împărțiți-al doilea rând de 3, și apoi să continue să se transforme înapoi metoda de substituție:

$$ \ stânga (\ începe 1 2 5 2 -3 \\ 0 3 -6 0 -4 \ end \ dreapta) \ începe \ fantomă \\ II: 3 \ end \ rightarrow \ stânga (\ începe 1 2 5 2 -3 \\ 0 1 -2 0 -4/3 \ end \ dreapta) \ începe I-2 \ cdot II \\ \ fantomă \ end \ rightarrow \\ \ rightarrow \ left (\ începe 1 0 9 2 1/3 \\ 0 1 -2 0 -4/3 \ end \ dreapta). $$

Caracteristicile Matrix pentru a deveni un singur, completat Gauss. Soluția generală este găsit, rămâne doar să-l scrie. Dacă ne amintim că a patra coloană corespunde variabilei $ x_2 $, iar coloana a cincea - variabila $ $ X_4, obținem:

Am obținut soluția generală dată SLAE. Pentru a găsi o soluție de bază, aveți nevoie de toate variabilele libere sunt egale cu zero. Ie presupunând $ x_2 = 0 $ și $ x_4 = 0 $, avem:

Soluție $ x_1 = 9 $, $ x_2 = 0 $, $ x_3 = -2 $, $ x_4 = 0 și $ este soluția de bază pentru acest SLAE. În principiu, setarea variabilelor libere de alte valori, puteți obține alte soluții particulare ale acestui sistem. O astfel de număr infinit privat de soluții. De exemplu, luând $ x_2 = -4 $ și $ x_4 = 1 $, obținem o anumită soluție: \ $ din stânga \ x_1 = \ frac; \\ x_2 = -4; \\ x_3 = - \ frac; \\ x_4 = 1. \ End \ dreapta. $. Soluție de bază, pe care am găsit mai devreme - doar unul dintr-un număr infinit de soluții particulare date Slough.

Dacă doriți, soluția rezultată poate fi verificată. De exemplu, înlocuind $ x_1 = 9 + 2x_2- \ fracx_4 $ și $ x_3 = -2 \ fracx_4 $ în partea stângă a primei ecuații, obținem:

$$ 3x_1-6x_2 + 9x_3 + 13x_4 = 3 \ cdot \ stânga (9 + 2x_2- \ fracx_4 \ dreapta) -6x_2 + 9 \ cdot \ stânga (-2 \ fracx_4 \ dreapta) + 13x_4 = 9. $$

Verificarea primei ecuații fără succes; în același mod în care se poate verifica doua și a treia ecuații.

Răspuns. Soluția generală: $ \ left \ x_1 = 9 + 2x_2- \ fracx_4; \\ x_2 \ în R; \\ x_3 = -2 \ fracx_4; \\ . X_4 \ în R. \ final \ $ dreapta, soluție de bază este: $ \ left \ x_1 = 9; \\ x_2 = 0; \\ x_3 = -2; \\ x_4 = 0. \ End \ dreapta. $.

Rezolva sisteme liniare \ $ din stânga \ x_1-2x_2 + 4x_3 + 2x_5 = 0; \\ 4x_1-11x_2 + 21x_3-2x_4 + 3x_5 = -1; \\ -3x_1 + 5x_2-13x_3-4x_4 + x_5 = -2. \ End \ dreapta. $. În cazul în care sistemul este incert, specificați soluția de bază.

Un exemplu similar a fost deja rezolvată în subiect linia „metoda lui Kramer“ (Exemplul №4). Variabile $ X_4 $ și $ x_5 $ au fost transferate pe laturile dreaptă, iar apoi a folosit metoda standard de operare Kramer. Cu toate acestea, această metodă nu garantează soluții pentru a obține rezultate. De exemplu, am transporta unele variabile în partea dreaptă, iar determinantul rămas este egal cu zero, - atunci ce? Forța brută pentru a rezolva. ) Prin urmare, este mult mai convenabil de a utiliza transformarea metodei Gauss. ca în exemplul anterior.

$$ \ stânga (\ începe 1 -2 4 0 2 0 \\ 4 -11 21 -2 3 -1 \\ -3 5 -13 -4 1 -2 \ end \ dreapta) \ începe \ fantomă \\ II-4 \ cdot I \\ III + 3 \ cdot I \ end \ rightarrow \ stânga (\ începe 1 -2 4 0 2 0 \\ 0 -3 5 -2 -5 -1 \\ 0 -1 -1 -4 7 -2 \ end \ dreapta) \ rightarrow \\ \ rightarrow \ din stânga | \ începe \ Text \\ \ Text \\ \ Text \ final \ dreapta | \ rightarrow \ left (\ începe 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ -3 5 -2 -5 -1 \ end \ dreapta) \ începe \ fantomă \\ \ fantomă \\ III-3 \ cdot I \ end \ rightarrow \\ \ rightarrow \ stânga (\ începe 1 -2 4 0 2 0 \\ 0 -1 -1 -4 7 -2 0 \\ 0 8 10 -26 5 \ end \ dreapta). $$

Sistemul de matrice și avansate matricea sistemului sunt reduse la o formă trapezoidală. Note ale acestor matrice sunt egale între ele și egale cu numărul 3, adică $ \ A = Rang \ sunat \ widetilde = 3 $. Deoarece rândurile sunt egale sau mai mic decât numărul de variabile, în funcție de investigarea Kronecker-Capelli, acest sistem are un număr infinit de soluții.

Numărul de $ n = necunoscutelor 5 $, rândurile ambelor matrici $ r = 3 $, deci trebuie să alegeți trei variabile de bază și $ n-r = $ 2 variabile gratuite. Aplicând același „etape“, metoda, la fel ca în exemplul anterior, vom alege ca variabile de bază $ x_1 $, $ x_2 $, $ x_3 $, precum și variabile gratuite - $ x_4 $ și $ x_5 $.

Coloanele №4 și №5, care corespund variabilelor libere, rapid înainte peste linia. Apoi împărțiți linia a treia 8 și extinde soluția metoda Gauss:

$$ \ stânga (\ începe 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 8 5 -10 26 \ end \ dreapta) \ începe \ fantomă \\ \ fantomă \\ III: 8 \ end \ rightarrow \ left (\ începe 1 -2 4 0 0 -2 0 \\ -1 -1 -2 4 -7 \\ 0 0 1 5/8 -5/4 13/4 \ end \ dreapta) \ begin I-4 \ cdot III \\ II + III \\ \ fantomă \ end \ rightarrow \\ \ stânga (\ începe 1 -2 0 -5/2 5 -15 \\ 0 -1 0 -11/8 11/4 -15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ dreapta) \ începe \ fantomă \\ II \ cdot (-1) \\ \ fantomă \ end \ rightarrow \ left (\ începe 1 -2 0 -5/2 5 -15 \\ 0 1 0 11/8 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ dreapta) \ begin I + 2 \ cdot II \\ \ fantomă \\ \ fantomă \ end \ rightarrow \\ \ rightarrow \ stânga (\ începe 1 0 0 1/4 -1/2 -15/2 \\ 0 1 0 11/8 -11/4 15/4 \\ 0 0 1 5/8 -5/4 13/4 \ end \ dreapta) $$

Din ultimul matricei au o soluție comună pentru un anumit sisteme liniare: \ $ din stânga \ x_1 = \ fracturate \ fracx_4- \ fracx_5; \\ x_2 = \ fracturate \ fracx_4 + \ fracx_5; \\ x_3 = \ fracturate \ fracx_4 + \ fracx_5; \\ x_4 \ în R; \\ x_5 \ în R. \ final \ dreapta. $. Soluție de bază este obținută în cazul variabilelor libere echivalează cu zero, adică $ X_4 = 0 $, $ x_5 = 0 $:

Continuarea acestei teme, ia în considerare a doua parte. Să examinăm în cazul în care încă două exemple de găsire a unei soluții comune.