3) minori și cofactori
razlozheniya.Minormatritsy formule A - determinantul unei matrice pătratică de ordinul k (care este, de asemenea, numit ordinul minorului), care sunt elemente ale matricei A la intersecția numerelor rând și numerele de coloane.
În cazul în care liniile de numere de potrivire marcate cu numere marcate coloane, numit principalul minor. iar dacă a marcat primele rânduri k și primele coloane k - unghiulare sau de conducere șef.
matrice element de comandă opțională minor n-lea este determinantul de ordinul (n-1), care corespunde celei de matrice, care se obține din matricea prin ștergerea rândului i-lea și coloana j-a.
minor de bază a matricei este oricare dintre nenulă minor sale de ordin maximal. Pentru Minor era de bază, este necesar și suficient ca toți minorii limitrofa (adică, conținând minori sale cu un grad mai mare de) au fost zero. Sistemul de linii (coloane) ale matricei asociate cu minorul de bază, este maximă liniar subsistem independent de toate rândurile matricei (coloane).
De exemplu, o matrice:
Să presupunem că doriți să găsiți un minor suplimentar. Acest minor - determinantul matricei, care se obține prin ștergerea rândului 2 și coloana 3:
Cofactor din numărul matritsynazyvaetsya elementului
,
în cazul în care - Minor suplimentare. determinant al matricei obținute din original matricea cu anulare de rândul i-lea și jth coloanei.
Numele de „cofactor“ este legată de formule de descompunere a determinantului unei linii matrice (în coloana):
Lema privind extinderea unei afirmații false determinante care
Aceste declarații trebuie algoritm pentru identificarea matricea inversă:
înlocuiți fiecare element al matricei originale la cofactor sale,
transpusa matricea rezultată - matrice adjugate se obține ca rezultat,
împărțiți fiecare element al matricei Uniunii asupra determinantul matricei originale.
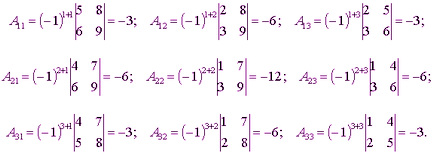
determinant
Introducem definiția determinantul unei matrice pătratică de ordine arbitrară. Această definiție este recursivă. care este, pentru a determina ce este determinantul matricei de ordine, trebuie să știi ce este determinantul matricei de ordine. De asemenea, observăm că există doar determinantul matricilor pătrate.
Determinantul unei matrice pătrată va fi notată sau det.
Determinarea 1.Opredelitelem matrice pătratică se numește numărul de ordinul doi.
Determinant unei matrice pătratică de ordine, denumit număr
în care - ordinul determinantul matricei obținută din matrice prin ștergerea primului rând și coloană cu numărul.
Pentru claritate, vom scrie, cum să calculeze determinantul matricei patra comandă:

Notă. Calculul efectiv al determinanților matrici mai mari decât al treilea ordin bazat pe definiția utilizată în cazuri excepționale. Ca regulă generală, calculul este efectuat pentru alți algoritmi, care vor fi discutate mai târziu, și care necesită mai puțin efort de calcul.
Notă. În definiția 1 ar fi mai corect să spunem că determinantul este o funcție definită pe mulțimea matricelor pătrate de ordine și valori într-un set de numere.
Notă. În literatura de specialitate, în loc de termenul „determinant“ folosit, de asemenea, termenul „determinant“, având același înțeles. Din cuvântul „determinant“ și a existat o Det notație.
Luați în considerare unele dintre proprietățile determinanților, care este formulat ca declarații.
Propoziția 1. Dacă transpune determinantul nu se schimbă, adică.
Revendicarea 2. Produsul este determinant Matricele pătrat este produsul factorilor determinanților, adică.
Propoziția 3. Dacă matricea de swap două rânduri, apoi modificările determinante semnează.
Declarație 4. Dacă matricea are două rânduri identice, determinant său este zero.
În viitor, vom avea nevoie pentru a adăuga o linie și se înmulțește cu numărul de coarde. Aceste acțiuni pe rânduri (coloane), vom efectua precum și acțiunile unei matrice rând (matricea coloană), adică elementul, cu element. Rezultatul va servi rând (coloană), ca regulă, nu coincide cu liniile matricei originale. Dacă există rânduri de adăugiri (coloana) și multiplicarea lor cu numărul putem vorbi de o combinație liniară de rânduri (coloane), adică suma coeficienților numerice.
Propoziția 5. Dacă un rând al matricei este înmulțită cu un număr, apoi determinant său este multiplicat cu acest număr.
Declarație 6. Dacă matricea conține un șir nul, atunci determinantul său este zero.
Adoptarea 7. Dacă una dintre celelalte rânduri ale matricei se înmulțește cu numărul (proporțional cu linia), atunci determinantul matricei este egal cu zero.
Adoptarea 8. Fie matricea i-lea rând are forma. Apoi, în cazul în care matricea obținută din matrice prin înlocuirea rând i-lea la rând, iar matricea - înlocuind rând i-lea la rând.
Propoziția 9. Dacă unul dintre rândurile matricei pentru a adăuga un alt, înmulțită cu numărul, determinantul matricei nu se schimbă.
Propoziția 10. Dacă unul dintre rândurile matricei este o combinație liniară a celuilalt rând că determinantul matricei este egal cu zero.
Determinarea 2.Algebraicheskim plus față de elementul matricei este un număr egal unde - determinantul matricei obținută din matrice prin ștergerea rândului i-lea și coloana j-a. este indicat adăugarea algebric la elementul de matrice.
Exemplu. Să. atunci
Notă. Folosind cofactori, Definiție 1 factor determinant poate fi scris ca:
4) și calculul acesteia matricei inverse. Inversa Matricea - un rezultat matrice de multiplicare pe care matricea inițială este matricea identitate.
Pentru a calcula matricea inversă, introduceți valoarea numărului de rânduri ale matricelor și numărul de coloane și apoi introduceți valorile elementelor matricei și apoi apăsați butonul „calculează“. Rezultatele programului vor fi matricea inversă. Matricea inițială și matricea inversă calculată poate fi copiat în clipboard pentru a fi utilizate în alte aplicații.